Birefringence: Difference between revisions
| Line 16: | Line 16: | ||
Salts can crystallize in different [[Crystal system|crystal systems]] depending on the arrangement of their ions in the crystal lattice. Each type of crystal lattice structure will have different optical properties. | Salts can crystallize in different [[Crystal system|crystal systems]] depending on the arrangement of their ions in the crystal lattice. Each type of crystal lattice structure will have different optical properties. | ||
When light passes through the lattice of optically anisotropic materials, it splits into two | When light passes through the lattice of optically anisotropic materials, it splits into two waves with different speeds and thereby differing refractions. This phenomenon is called double refraction or birefringence (delta) and was first observed on calcite crystals around the mid 17th century. | ||
When light waves enter an anisotropic medium, not only birefringence, but also polarization takes place: both | When light waves enter an anisotropic medium, not only birefringence, but also polarization takes place: both waves are altered in their vibration mode to such a degree that they are oriented perpendicularly to each other and vibrate only in one direction, i.e., they are linearly polarized. | ||
In an isotropic material the light waves have the same velocity in all directions. Only materials that crystallize in the cubic system are isotropic. When imagining a model, in which light radiates from the center of such a crystal into all directions, the shape of the light would form a sphere in the case of isotropic materials. This model is called indicatrix. | In an isotropic material the light waves have the same velocity in all directions. Only materials that crystallize in the cubic system are isotropic. When imagining a model, in which light radiates from the center of such a crystal into all directions, the shape of the light would form a sphere in the case of isotropic materials. This model is called indicatrix. | ||
Revision as of 20:26, 5 January 2014
Authors: Hans-Jürgen Schwarz, Anika Husen
English version by Sandra Leithäuser
back to Polarized light microscopy
Abstract[edit]
Birefringence or double refraction refers to the phenomenon that occurs when a ray of light ray splits into two when passing into an optically anisotropic medium. The two light rays have different speeds, depending on the direction of the wave propagation within the body. One of these rays is refracted normally (ordinary ray) and the other undergoes a change in direction (extraordinary ray). The path difference that arises between the speed of the two rays leads to interference colors. The majority of salts are anisotropic, i.e., a light ray will experience birefringence when passing through them. Salts crystallizing in the cubic system are isotropic.
Anisotropic crystals[edit]
Salts can crystallize in different crystal systems depending on the arrangement of their ions in the crystal lattice. Each type of crystal lattice structure will have different optical properties.
When light passes through the lattice of optically anisotropic materials, it splits into two waves with different speeds and thereby differing refractions. This phenomenon is called double refraction or birefringence (delta) and was first observed on calcite crystals around the mid 17th century.
When light waves enter an anisotropic medium, not only birefringence, but also polarization takes place: both waves are altered in their vibration mode to such a degree that they are oriented perpendicularly to each other and vibrate only in one direction, i.e., they are linearly polarized.
In an isotropic material the light waves have the same velocity in all directions. Only materials that crystallize in the cubic system are isotropic. When imagining a model, in which light radiates from the center of such a crystal into all directions, the shape of the light would form a sphere in the case of isotropic materials. This model is called indicatrix.
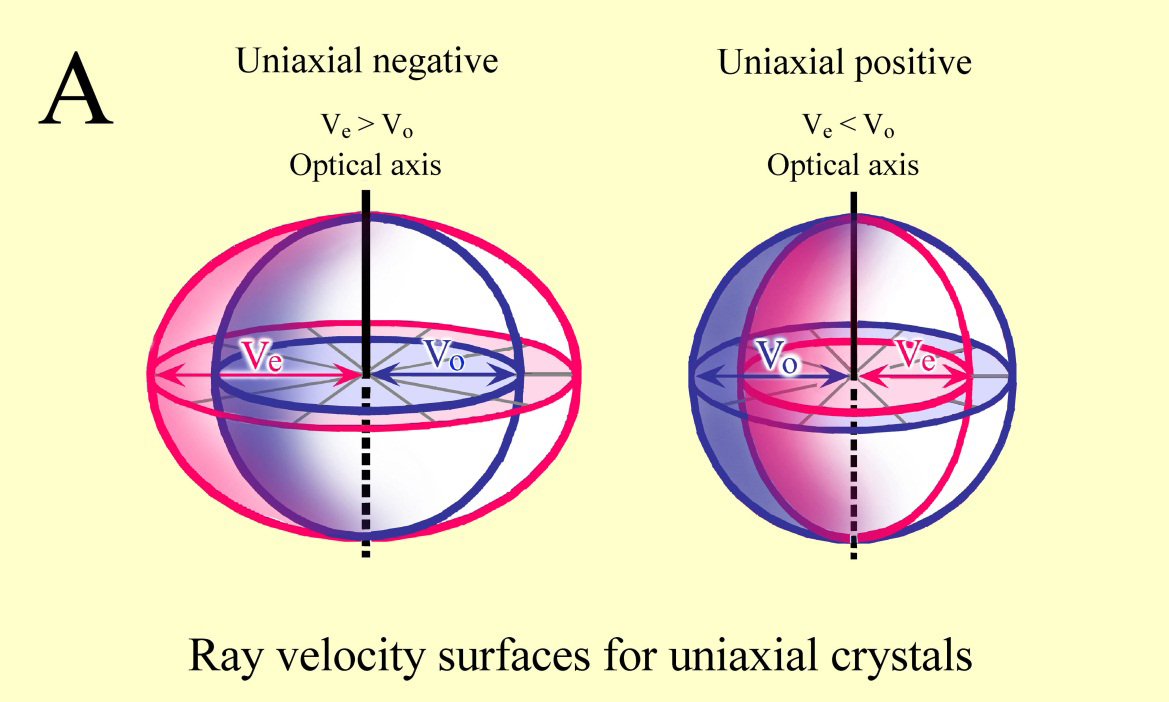
The indicatrix for hexagonal, trigonal and tetragonal crystal systems exhibits a unixial ellipsoid of revolution. These minerals are described as optically uniaxial.
The indicatrix of rhombic, monoclinic and triclinic crystal systems is an ellipsoid with two optical axes, because the speed of light is different along the three axes. Minerals belonging to these systems are called biaxial.
Refractive Index- birefringence[edit]
The term optical density (absorbance) is used to describe the light velocity in a medium. Materials with a higher optical density have a lower speed of light. The value of the refraction/refractive index corresponds to the ratio of the speed of light in vacuum to that in the material in question. The speed of light in vacuum is fastest, so that all refractive indices of materials are smaller than 1. The difference between the highest and lowest refractive index of a crystal is known as birefringence.
| nx = Refraction index of light, CLight = Speed of light in the vacuum, cx = Speed of light in the material X |
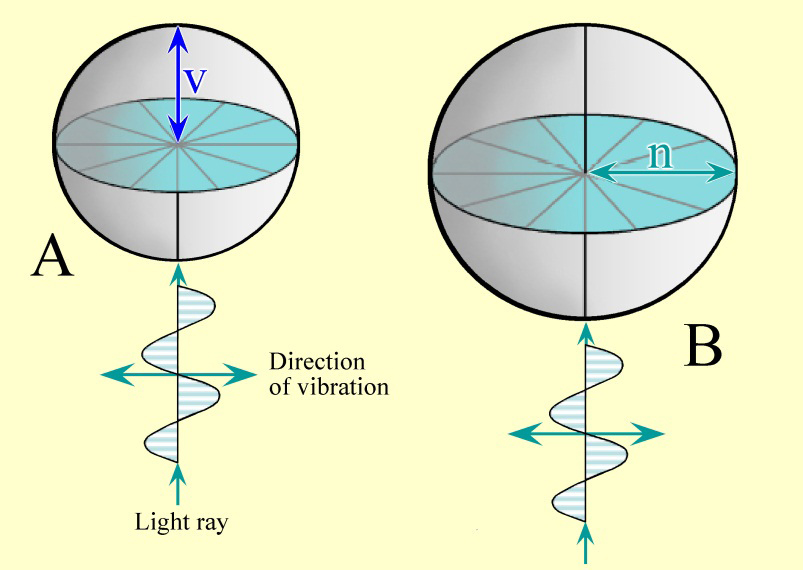
Author: Raith, Michael M.; Raase, Peter; Reinhardt, Jürgen

Birefringence takes place on optically anisotropic (non-cubic) crystals, but it differs from the simple refraction of light. Refraction of light takes place at every boundary surface, between varying optically dense media, causing a deflection of the ray direction and the splitting into spectral colors. Birefringence is associated with both a change in wavelength and the change of direction.
When birefringence takes place, the polarized light at the boundary surface of the crystal is split into two light paths. These undergo a change in polarization along the perpendicularly orientated transmission planes, forming the ordinary and extraordinary rays. The ordinary ray is refracted with the constant refractive index (no). The extraordinary ray has its polarization direction perpendicular to the ordinary ray and a refractive index (ne), that is dependent of its direction inside the crystal. The graphical representation of the different refractive indices into all spacial directions is the indicatrix.
Author: Raith, Michael M.; Raase, Peter; Reinhardt, Jürgen

The refractive indices are shown as vectors taken from one point into all directions, their length being proportional to their respective refractive index. When looking at optically uniaxial crystals, the indicatrix forms a spheroid with the optical axis being the axis of the ellipsoid. The indicatrix of optically biaxial crystals forms a complicated double-shell model, while cubic systems produce a sphere.
Ordinary- extraordinary ray[edit]
Between the two rays that travel at different speeds, a path difference or retardation occurs. The path difference leads to a positive interference for the wave length, and the integer multiple of the wave lengths causes the retardation. Therefore the crystal appears in a specific color, designated as an interference color.
Extinction[edit]
The orientation of the vibration plane of the crystal will determine whether it is located in the dark (extinct) or in the bright position. The dark position re-appears four times every 90°, when rotating the crystal on the stage. In this position the transmission directions of the crystals are the same as the direction of the microscope polarizers. This results in the light not being re-polarized by the crystal, because light rays already vibrate inside a transmission plane, when they strike the crystal. Thus, the extraordinary ray is eliminated and the light meets the analyzer with simple polarization and perpendicular to its transmission plane. For this reason, the light, that has passed through the crystal this way, does not pass through the analyzer and does not contribute to the visible image. This phenomenon is called extinction.
When the crystal is oriented so that none of its transmission planes are parallel to the polarizer, birefringence or double refraction takes place. The elliptically polarized light that passes through the analyzer goes into a vibration plane that makes the crystal visible. The color of the crystal is the result of the retardation produced. The retardation is determined by the difference of the refractive indices in the direction of light transmission and therefore the value of birefringence. The intensity of the retardation is also affected by the thickness of the crystal, i.e., the distance the ray has to travel within the material.
The orientation of the dark position depends on the properties of the crystal lattice and it is therefore possible to draw conclusions about the crystal system. If, in the dark position, the crystal exhibits a parallel or perpendicular orientation towards the horizontal line, which is recognizable through the orientation of the cleavage planes or the habit, this is referred to as symmetrical or parallel extinction. If the orientation is in the dark position, but not parallel nor perpendicular to the horizontal line, the extinction behavior is called inclined extinction. Estimating the extinction angle can help to accurately identify a mineral.
Interference colors[edit]
In order to identify a phase, the examination of interference colors can be useful. These become visible under crossed polars and occur due to retardation, which is produced by birefringence. Depending on the magnitude of the retardation, the crystal appears in a specific color in the dark field. The appearing color is linked to the wavelength, which undergoes a positive interference due to the retardation of the doubly refracted light. Hence, color and retardation are dependent on the refractive indices and on the thickness of the crystal. If the approximate thickness of the crystal is known, the refractive indices can be estimated by examining the interference colors. For this purpose, the bright position, i.e., the maximum birefringence is examined. The use of a color chart after Michel-Lévy [1] is recommended. It shows the correlation between interference colors with respect to the retardation or the refractive indices as a function of the thickness of the object.
Weblinks[edit]
- ↑ http://www.zeiss.com/C1256CFB00332E16/0/FECC5775A0897BCCC1256D08002A4E39/$file/46-0014_d.pdf accessed July 28, 2010
Literature[edit]
| [Raith.etal:2012] | Raith, Michael M.; Raase, Peter; Reinhardt, Jürgen (2012): Guide to Thin Section Microscopy, Second Edition, online publication, Url, |  |
