Dew point

back to Measured Variables

This page contains contents from http://en.wikipedia.org/wiki/Dew_point (28.10.2012) it is therefore released under the licence: „Creative Commons Attribution/Share Alike“

with contributions by Sandra Leithäuser

Dew point

Figure 1 Phase transition of water
(Wasser-Water; Eis-Ice; Wasserdampf-Water vapor; Druck-Pressure; Kritischer Punkt-Critical point; Tripelpunkt- Triple point)

Figure 2 Maximum water vapor concentration as a function of temperature

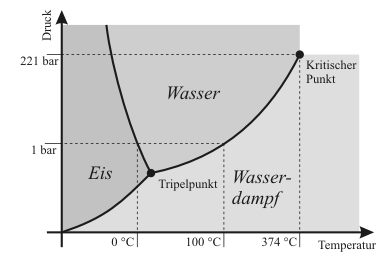
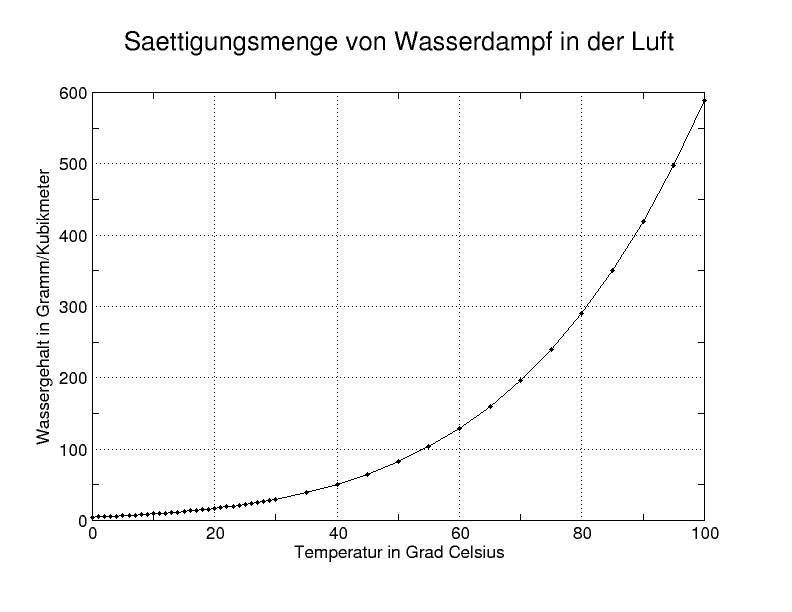
Dew point is the temperature below which the water vapor present in a volume of humid air at a constant barometric pressure will condense to liquid water. Condensed water is called dew when it forms on a solid surface.

The dew point is a water-to-air saturation temperature. It is associated with relative humidity, so a high relative humidity indicates that the dew point is closer to the current air temperature. Relative humidity of 100% indicates the dew point is equal to the current temperature and that the air is saturated with water. When the dew point remains constant and temperature increases, relative humidity decreases.

At a given temperature but independent of barometric pressure, the dew point is a consequence of the absolute humidity, the mass of water per unit volume of air. If both the temperature and pressure rise, however, the dew point will rise and the relative humidity will lower accordingly. Reducing the absolute humidity without changing other variables will bring the dew point back down to its initial value. In the same way, increasing the absolute humidity after a temperature drop brings the dew point back down to its initial level. If the temperature rises in conditions of constant pressure, then the dew point will remain constant but the relative humidity will drop. For this reason, a constant relative humidity (%) with different temperatures implies that when it is hotter, a higher fraction of the air is water vapor than when it is cooler.

At a given barometric pressure but independent of temperature, the dew point indicates the mole fraction of water vapor in the air, or, put differently, determines the specific humidity of the air. If the pressure rises without changing this mole fraction, the dew point will rise accordingly; Reducing the mole fraction, i.e., making the air less humid, would bring the dew point back down to its initial value. In the same way, increasing the mole fraction after a pressure drop brings the relative humidity back up to its initial level.

For example, considering New York (33 ft elevation) and Denver (5,280 ft elevation), this means that if the dew point and temperature in both cities are the same, then the mass of water vapor per cubic meter of air will be the same, but the mole fraction of water vapor in the air will be greater in Denver.

Measurement

Dew point meters are devices used to measure the dew point over a wide range of temperatures. They consist of a polished metal mirror which is cooled as air is passed over it. The temperature at which dew forms is, by definition, the dew point. Manual devices of this sort can be used to calibrate other types of humidity sensors, and automatic sensors may be used in a control loop with a humidifier or dehumidifier to control the dew point of the air in a building or in a smaller space for a manufacturing process.

See Moisture measurement methods for more detail.

Calculating the dew point

A well-known approximation used to calculate the dew point, T_dp, is the Magnus formula below, based on the actual ("dry bulb") air temperature, T and percent relative humidity RH: Failed to parse (syntax error): {\displaystyle \gamma(T,R\!H)&=\ln\left(\frac{R\!H}{100}\exp\!\!\left(\frac{bT}{c+T}\right)\right)=\ln\left(\frac{R\!H}{100}\right)+\frac{bT}{c+T};\\ T_{dp}&= \frac{c\gamma(T,R\!H)}{b-\gamma(T,R\!H)} }

The origin of this approximation involves a more complete formula that interrelates saturated water vapor pressure (in units of bar millibar, which is also hPa at T, P_s(T), and the actual water vapor pressure (also in units of millibar), P_a(T), which can be either found with RH or approximated with the barometric pressure (in millibar units), BP_mb, and "wet-bulb" temperature, T_w is:

Note: unless declared otherwise, all temperatures are expressed and worked in degrees Celsius

Failed to parse (syntax error): {\displaystyle P_s(T)& = \frac{100}{R\!H}P_\text{a}(T) = a\exp\!\!\left(\frac{bT}{c+T}\right);\\[8pt] P_\text{a}(T) & = \frac{R\!H}{100}P_s(T)=a\exp(\gamma(T,R\!H)),\\ &\approx P_s(T_\text{w}) - B\!P_\text{mb} 0.00066 \left[1 + (0.00115T_\text{w} \right)]\left(T-T_\text{w}\right);\\[5pt] T_\text{dp} & = \frac{c\ln(P_\text{a}(T)/a)}{b-\ln(P_\text{a}(T)/a)}}

For greater accuracy, P_s(T) (and, therefore, γ(T,RH)) can be enhanced, using part of the Bögel modification, also known as the Arden Buck equation, which adds a fourth, d constant:

Failed to parse (syntax error): {\displaystyle P_{s:m}(T)&=a\exp\!\!\bigg(\left(b-\frac{T}{d}\right)\left(\frac{T}{c+T}\right)\bigg);\\[8pt] \gamma_m(T,R\!H)&=\ln\Bigg(\frac{R\!H}{100}\exp\!\! \bigg(\left(b-\frac{T}{d}\right)\left(\frac{T}{c+T}\right)\bigg) \Bigg);\\ T_{dp}&= \frac{c\gamma_m(T,R\!H)}{b-\gamma_m(T,R\!H)}}

(where $\scriptstyle {a=6.1121;\quad \;b=18.678;\quad \;c=257.14^{\circ }C;\quad \;d=234.5^{\circ }C.}$)

There are several different constant sets in use, the ones used in NOAA's presentation are taken from a 1980 paper by David Bolton in the Monthly Weather Review:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a&=6.112;\quad\;b&= 17.67;\quad\;c&= 243.5^\circ C;}

These values provide a minimum accuracy of 0.1%, for

-30°C ≤ T ≤ +35°C;

1% < RH < 100%;

Also noteworthy is the Sonntag1990,

$\scriptstyle {a=6.112;\quad \;b=17.62;\quad \;c=243.12^{\circ }C:\quad -45^{\circ }C\leq T\leq +60^{\circ }C\quad (<-0.35^{\circ }C)}$

Another common set of values originates from the 1974 Psychrometry and Psychrometric Charts, as presented by Paroscientific,

$\scriptstyle {a=6.105;\quad \;b=17.27;\quad \;c=237.7^{\circ }C:\quad 0^{\circ }C\leq T\leq +60^{\circ }C\quad (\pm 0.4^{\circ }C)}$

Also, in the Journal of Applied Meteorology and Climatology, Arden Buck presents several different valuation sets, with different minimum accuracies for different temperature ranges. Two particular sets provide a range of -40°C → +50°C between the two, with even greater minimum accuracy than all of the other, above sets (maximum error at given |C°| extreme):

$\scriptstyle {a=6.1121;\quad \;b=17.368;\quad \;c=238.88^{\circ }C:\quad \quad \!0^{\circ }C\leq T\leq +50^{\circ }C\;\;(\leq 0.05\%)}$

$\scriptstyle {a=6.1121;\quad \;b=17.966;\quad \;c=247.15^{\circ }C:\quad -40^{\circ }C\leq T\leq 0^{\circ }C\quad \!\;\;(\leq 0.06\%)}$

Simple approximation

There is also a very simple approximation that allows conversion between the dew point, temperature and relative humidity. This approach is accurate to within about ±1°C as long as the relative humidity is above 50%:

$T_{dp}\approx T-{\frac {100-R\!H}{5}};$

and

$R\!H\approx 100-5(T-T_{dp});\,$

This can be expressed as a simple rule of thumb:

For every 1°C difference in the dew point and dry bulb temperatures, the relative humidity decreases by 5%, starting with RH = 100% when the dew point equals the dry bulb temperature.

The derivation of this approach, a discussion of its accuracy, comparisons to other approximations, and more information on the history and applications of the dew point are given in the Bulletin of the American Meteorological Society.

For temperatures in degrees Fahrenheit, these approximations work out to

$T_{dp:f}\approx T_{f}-{\frac {9}{25}}(100-R\!H);$

and

$R\!H\approx 100-{\frac {25}{9}}(T_{f}-T_{dp:f});$

For example, a relative humidity of 100% means dew point is the same as air temp. For 90% RH, dew point is 3 degrees Fahrenheit lower than air temp. For every 10 percent lower, dew point drops 3 °F.

Frost point

The frost point is similar to the dew point, in that it is the temperature to which a given parcel of humid air must be cooled, at constant barometric pressure, for water vapor to be deposited as ice on a surface without going through the liquid phase. The frost point for a given parcel of air is always higher than the dew point, as the stronger bonding between water molecules on the surface of ice requires a higher temperature to break.

External links

• What is the dew point?
• Dew point definition NOAA Glossary
• Dew point formula
• Often Needed Answers about Temp, Humidity & Dew Point from the sci.geo.meteorology
• Humidity calculator
• Dew point calculator in construction

A phase is a physically distinctive form of matter and is characterized by having relatively uniform chemical and physical properties.

relative humidity