Salts/Salt Mixtures: Difference between revisions
No edit summary |
|||
| (82 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
Author: [[ | Author: [[user:AmelieStahlbuhk|Amelie Stahlbuhk]] | ||
<br> | <br> | ||
back to [[ | back to [[Saltwiki:Community portal]] | ||
<br> | <br> | ||
| Line 9: | Line 9: | ||
==Salts in cultural heritage objects== | ==Salts in cultural heritage objects== | ||
Salts are based on ionic compounds, having both positively charged ions ( | Salts are based on ionic compounds, having both positively charged ions (cations) and a negatively charged ions (anions). Both cations and anions can have one or more positive or negative charges but they must balance out in the salt. Cultural heritage objects of porous, inorganic materials, such as buildings monuments, may be contaminated with salts. The most common cations are sodium (Na<sup>+</sup>), potassium (K<sup>+</sup>), magnesium (Mg<sup>++</sup>) and calcium (Ca<sup>++</sup>). For the case of anions, the most frequently found are chloride (Cl<sup>-</sup>), sulfate (SO<sub>4</sub><sup>=</sup>), nitrate (NO<sub>3</sub><sup>-</sup>)and carbonate (CO<sub>3</sub><sup>=</sup>). Depending on the environment of the object, origin of the salts and past restorations/conservation measure, there may be other cations present, such as barium (Ba<sup>++</sup>) or ammonium (NH<sub>4</sub><sup>+</sup>), or anions, such as acetate (CH<sub>3</sub>COO<sup>-</sup>). The latter one is particularly relevant in the case where objects, such as ceramics, are displayed or stored in wooden cases which emit acetic acid over time, resulting in the efflorescence of an acetate salt, such as sodium or potassium from the object itself. In the case of metal objects, other cations may also appear. The following section will focus mainly on the most common minerals. | ||
==Single, double or triple salt== | ==Single, double or triple salt== | ||
Salts can be differentiated depending on the number of cations or anions they contain. If there is only one cation and one anion, such as | Salts can be differentiated depending on the number of cations or anions they contain. If there is only one cation and one anion, such as in sodium chloride [[Halite | NaCl]], then it is a single salt. An example of a double salt could be that of darapskite, which contains only one cation, sodium, but two different anions, sulfate and nitrate (Na<sub>3</sub>(SO<sub>4</sub>)(NO<sub>3</sub>)∙H<sub>2</sub>O) as well as aphtitalite, which has two cations sodium and potassium, but only one anion, sulfate (K<sub>3</sub>Na(SO<sub>4</sub>)<sub>2</sub>). However, this formula could also be written as follows: Na<sub>2</sub>SO<sub>4</sub>∙3K<sub>2</sub>SO<sub>4</sub> or (K<sub>3</sub>Na(SO<sub>4</sub>)<sub>2</sub>), the former showing that the salt is actually composed by a combination of two single salts. <br> | ||
However, this formula could also be written as follows: Na<sub>2</sub>SO<sub>4</sub>∙3K<sub>2</sub>SO<sub>4</sub> or (K<sub>3</sub>Na(SO<sub>4</sub>)<sub>2</sub>), the former showing that the salt is actually composed by a combination of two single salts. <br> | |||
Some double salts may be found on building materials | Some double salts may be found on building materials, these may form depending on environmental conditions, as well as triple salts; the latter, according to the definition may have three different cations or anions, however, these are not found as frequently. <br> | ||
In the case of double salts, some may differentiate themselves depending on whether they have a congruent or incongruent solubility. In the case of a congruent solubility, when the salt dissolves in water, the solution will have the same mixture of anions and cations as the salt itself, and when it evaporates, the same salt will precipitate out. In the case of incongruent solubility, depending on the concentration of the produced solution, other phases may crystallize out, so that the solution will no longer have the same composition as the original salt | In the case of double salts, some may differentiate themselves depending on whether they have a congruent or incongruent solubility. In the case of a congruent solubility, when the salt dissolves in water, the solution will have the same mixture of anions and cations as the salt itself, and when it evaporates, the same salt will precipitate out. In the case of incongruent solubility, depending on the concentration of the produced solution, other phases may crystallize out, so that the solution will no longer have the same composition as the original salt, therefore, when the solution evaporates completely, the original salt will not necessarily be obtained, since some phases had separated previously. The crystallization and dissolution processes of incongruent salts is very complex and information regarding their solubility and crystallization processes is not easily predictable. | ||
==Salt | ==Salt solubility== | ||
Salts have distinct solubilities that are temperature dependent. For buildings contaminated by salts this is an important point, since the mobility of a particular salt will depend on its solubility | Salts have distinct solubilities that are temperature dependent. For buildings contaminated by salts this is an important point, since the mobility of a particular salt will depend on its solubility: those with lower solubility will crystallize sooner. Considering a wall with rising damp, where the ground water and the salts it contains, rises by capillarity, a fractionation of the salts can be detected. Salts with low solubility will crystallize out close to where the water enters the wall, while highly soluble salts may rise higher <bib id="Arnold.etal:1991"/>. | ||
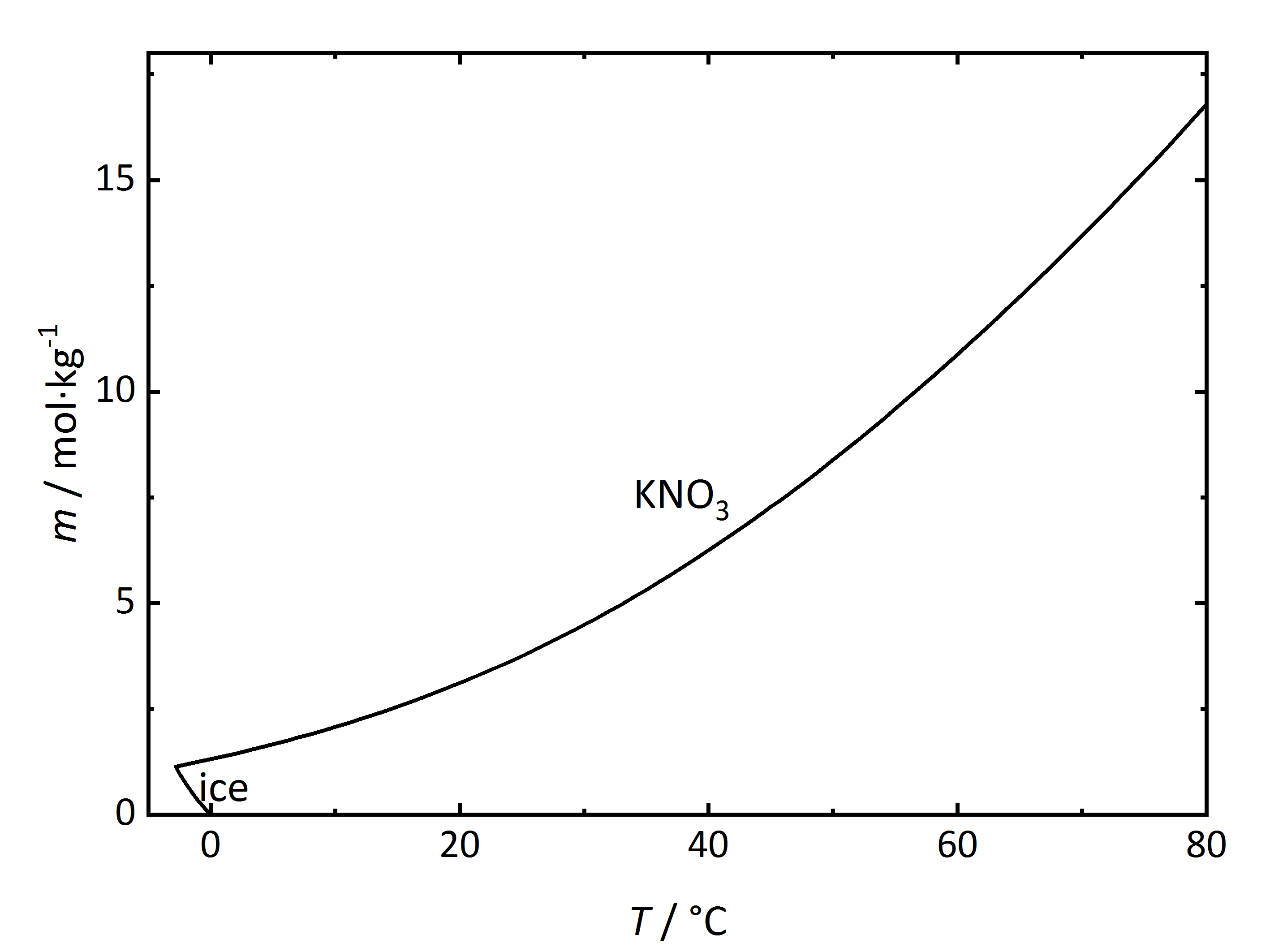
The solubility temperature dependence can be described by solubility diagrams. To illustrate the point the solubility diagram for a single salt, such as potassium nitrate, is shown in Fig. 1. In this diagram, the solubility of the salt in water is given by its concentration expressed in molality (mol/kg<sub>solvent</sub>, where the solvent | The solubility temperature dependence can be described by solubility diagrams. To illustrate the point the solubility diagram for a single salt, such as [[Niter | potassium nitrate]], is shown in Fig. 1. In this diagram, the solubility of the salt in water is given by its concentration expressed in molality (mol/kg<sub>solvent</sub>, where the solvent is water) on the ordinate axis as a function of temperature on the abscissa axis. The black line in the diagram reflects the saturation concentration of the salt as a function of the temperature. At 20°C, the solution of the [[Niter | potassium nitrate]] would have a molality of 3.1 mol/kg corresponding to a saturated solution. Below the line, the solution is not saturated, above the line the solution is saturated and salt will precipitate out. In the case of this salt, the solubility increases with temperature. At very low temperatures, ice will also crystallize out. | ||
[[File:KNO3 | [[File:Solubility KNO3.jpg|400px|thumb|left|'''Figure 1''': Solubility of [[Niter | potassium nitrate]] in water. The molality ''m'' [n(KNO<sub>3</sub>)•kg(H<sub>2</sub>O)<sup>-1</sup>] is plotted versus temperature ''T''.]] | ||
<br clear=all> | <br clear=all> | ||
| Line 44: | Line 43: | ||
In the above, the actual water vapor partial pressure is given by <i>p</i><sub>w</sub> and the saturation partial pressure is given by <i>p</i><sub>w,0</sub>, so that the water activity of a solution | In the above, the actual water vapor partial pressure is given by <i>p</i><sub>w</sub> and the saturation partial pressure is given by <i>p</i><sub>w,0</sub>, so that the water activity of a solution in equilibrium equals the air moisture above the solution. | ||
==Hydrated salts== | ==Hydrated salts== | ||
Some salts may crystallize both as anhydrous as well as hydrated | Some salts may crystallize both as anhydrous as well as hydrated phases with one or more water molecules, the latter being embedded into the crystal structure. [[Mirabilite]], Na<sub>2</sub>SO<sub>4</sub>∙10H<sub>2</sub>O forms from the system Na<sup>+</sup>-SO<sub>4</sub><sup>2-</sup>-H<sub>2</sub>O and crystallizes with ten water molecules inserted in the crystal, with a ratio of one mole Na<sub>2</sub>SO<sub>4</sub> to ten moles H<sub>2</sub>O. A hydration reaction can be postulated similarly to a solubility reaction: | ||
M<sub><i>ν</i>,M</sub>X<sub><i>ν</i>,X</sub>•<i>ν</i><sub>0,A</sub>H<sub>2</sub>O+(<i>ν</i><sub>0,B</sub>-<i>ν</i><sub>0,A</sub>)H<sub>2</sub>O<sub>(g)</sub> ⇌ M<sub><i>ν</i>,M</sub>X<sub><i>ν</i>,X</sub>•<i>ν</i><sub>0,B</sub>H<sub>2</sub>O (Eq. 4) | M<sub><i>ν</i>,M</sub>X<sub><i>ν</i>,X</sub>•<i>ν</i><sub>0,A</sub>H<sub>2</sub>O+(<i>ν</i><sub>0,B</sub>-<i>ν</i><sub>0,A</sub>)H<sub>2</sub>O<sub>(g)</sub> ⇌ M<sub><i>ν</i>,M</sub>X<sub><i>ν</i>,X</sub>•<i>ν</i><sub>0,B</sub>H<sub>2</sub>O (Eq. 4) | ||
| Line 56: | Line 55: | ||
<i>K</i><sub>H</sub>=<i>p</i><sub>w</sub><sup>0</sup>/<i>p</i><sub>w,AB</sub>=1/RH<sub>AB</sub> (Eq. 5) | <i>K</i><sub>H</sub>=<i>p</i><sub>w</sub><sup>0</sup>/<i>p</i><sub>w,AB</sub>=1/RH<sub>AB</sub> (Eq. 5) | ||
The saturation partial pressure, or deliquescence, <i>p</i><sub>w</sub><sup>0</sup> | The saturation partial pressure, or deliquescence, <i>p</i><sub>w</sub><sup>0</sup> is related to the water vapor pressure corresponding to the equilibrium between the lower (A) and the higher (B) hydration phase <i>p</i><sub>w,AB</sub>, resulting in the reciprocal value of the relative humidity (RH) in equilibrium with both phases, A and B, RH<sub>AB</sub>. When the RH increases above that for RH<sub>AB</sub> hydration of the salt will occur, while if the RH decreases below that value, dehydration will occur. <bib id="Steiger.etal:2014"/><bib id="Steiger:2009a"/>. | ||
RH<sub>AB</sub>. When the RH increases above that for RH<sub>AB</sub> hydration of the salt will occur, while if the RH decreases below that value, dehydration will occur. <bib id="Steiger.etal:2014"/><bib id="Steiger:2009a"/>. | |||
==Phase diagrams== | ==Phase diagrams== | ||
Salts with the general formula M<sup><i>z</i>+</sup>-X<sup><i>z</i>-</sup>-H<sub>2</sub>O (where M corresponds to the cations, and X to the anions, where several ions can be included, some having different charges z) can result in the formation of different phases depending on the temperature and relative humidity (RH). From the phase diagrams the stability conditions for the various phases can be determined. | |||
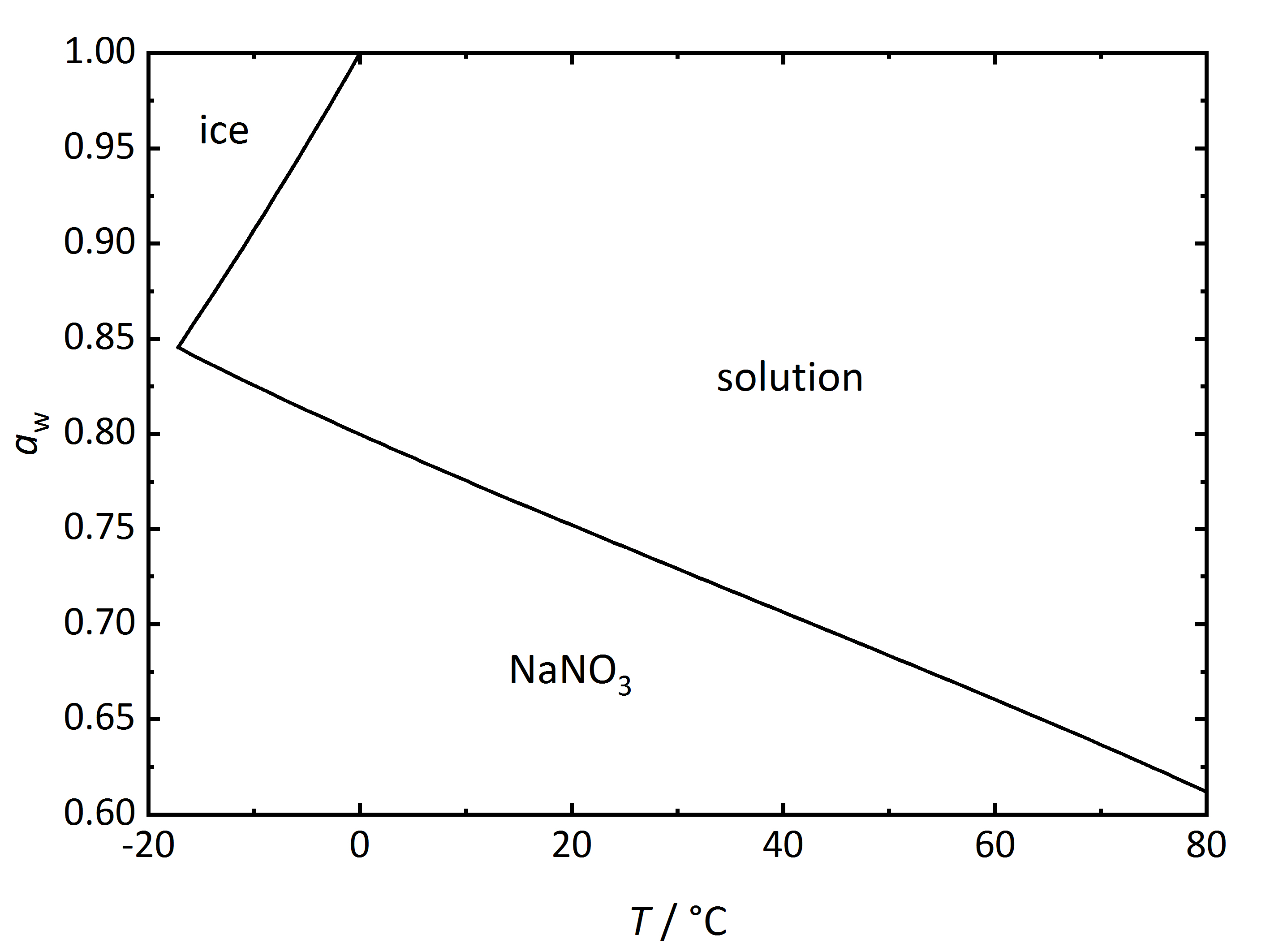
For the case of single salts that do not hydrate there is a specific relation between temperature and RH above which the salt will begin to absorb water vapor from the air to form a saturated solution. This point is defined as the deliquescence relative humidity (DRH), where the crystalline phase, the saturated solution and the water vapor above it are in equilibrium thus corresponding to the water activity of the solution. In the phase diagram for [[Nitronatrite | sodium nitrate]] shown in (Fig. 2) it can be seen that the DRH at a temperature of 20°C corresponds to 75.3 % RH. The diagram also shows that the DRH will decrease with increasing temperature. Above the line corresponding to the saturated salt solution, it can be seen that with increasing RH and at a given temperature the ongoing water vapor absorption will dilute the solution. On the other hand, with decreasing RH, the solution will concentrate as water vapor is released into the environment, until the salt reprecipitates upon reaching the DRH value. How much water will be absorbed above the DRH depends on the equilibrium between solution and water vapor in the environment, i.e., RH. In equilibrium, the water activity of the solution will correspond to the RH of the environment (Eq. 3). If humidity rises, the system will absorb more water vapor from the environment so that equilibrium is restored. | |||
[[File:NaNO3 | [[File:NaNO3 phase diagram.jpg|400px|thumb|left|'''Figure 2''': Phase diagram of the system Na<sup>+</sup>-NO<sub>3</sub><sup>-</sup>-H<sub>2</sub>O. The water activity <i>a</i><sub>w</sub> is plotted versus temperature ''T''. <bib id="Steiger.etal:2008c"/>]] | ||
<br clear=all> | <br clear=all> | ||
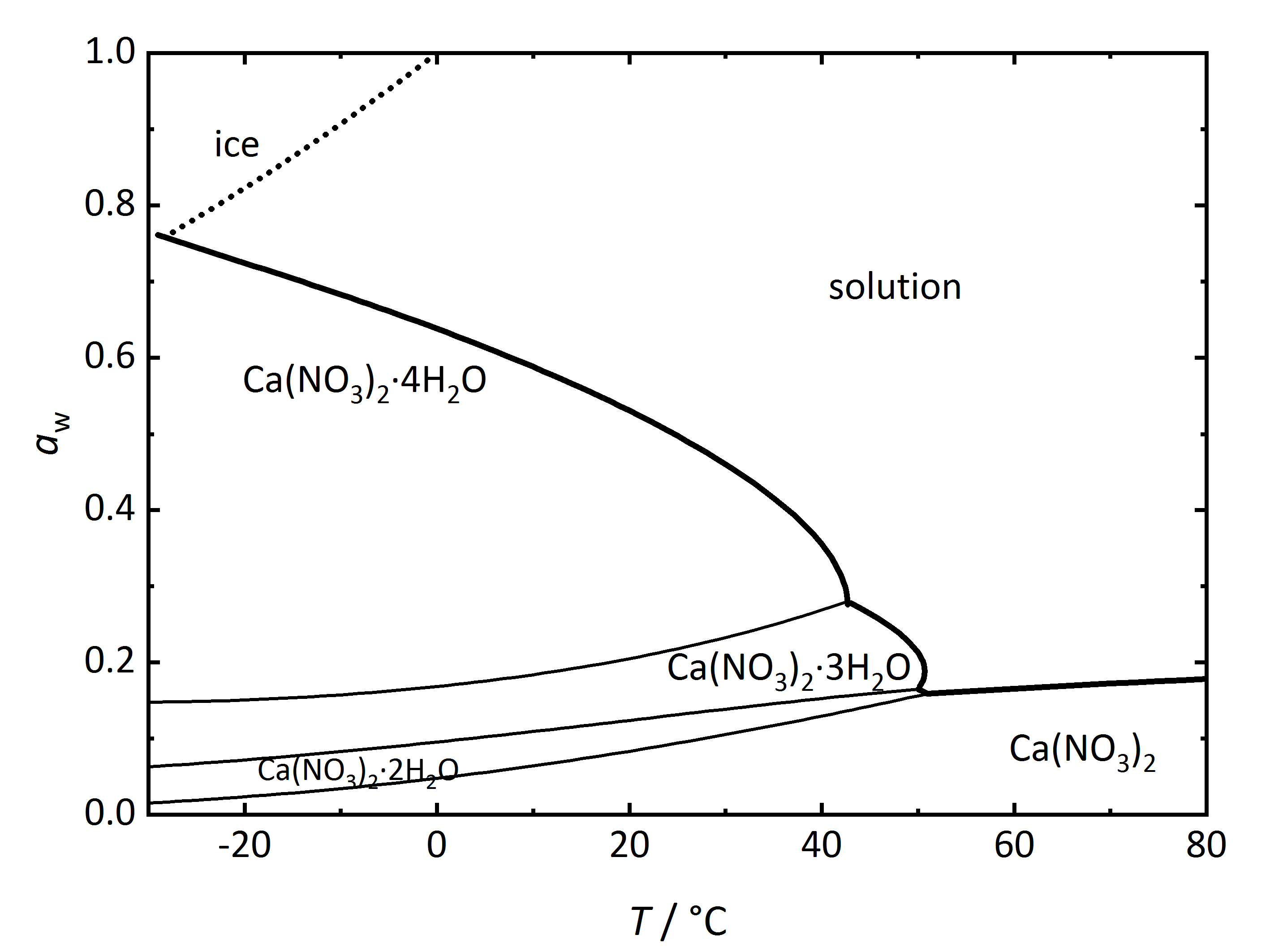
Apart from single salts, there are many salts which may have different hydrated phases. A relatively simple phase diagram to illustrate such a system is that corresponding to Ca<sup>2+</sup>-NO<sub>3</sub><sup>-</sup>-H<sub>2</sub>O (Fig. 3). In this case, three different hydration phases can be found apart from the anhydrous one. Similarly to the DRH that reflects the point where the salt will start to absorb water vapor to form a saturated solution, there is in this case a RH value where the anhydrous salt will absorb water to form a hydrated phase, and if more hydration phases can form, there will be several points. The phase diagram shows the different hydration phases that the salt can form. Different lines will show their stability areas. The different DRH for the hydrates are shown by the thicker drawn lines, and they describe the equilibrium between the crystalline salt, the saturated solution and the water vapor in the air. There are also other thinner lines that describe the phase changes between the various hydration-dehydration equilibria between the lower and higher hydration phases. It is also important to consider the formation of ice, which is shown by the dotted line. Thus, at temperatures below 0°C, the equilibrium with ice needs also to be considered together with that of the tetrahydrate calcium nitrate ([[nitrocalcite]]) <bib id="Steiger.etal:2014"/>. | |||
[[File:Ca(NO3)2 | [[File:Ca(NO3)2 phase diagram.jpg|400px|thumb|left|'''Figure 3''': Phase diagram of the system Ca<sup>2+</sup>-NO<sub>3</sub><sup>-</sup>-H<sub>2</sub>O. The water activity <i>a</i><sub>w</sub> is plotted versus temperature ''T''.]] | ||
<br clear=all> | <br clear=all> | ||
Phase diagrams for salts having several hydrates can be even more complex, so another example will be given for the system | |||
Na<sup>+</sup>-SO<sub>4</sub><sup>2-</sup>-H<sub>2</sub>O <bib id="Steiger.etal:2008"/> (Fig. 4). Again, thicker lines show the equilibrium between the saturated solution and the crystalline phase in question, corresponding to the DRH value. They grey line represents the dehydration or the hydration equilibrium between the anhydrous phase ([[thenardite]]) and the decahydrate ([[mirabilite]]). [[Mirabilite]] and [[thenardite]] are not stable at all temperatures, so that the transition temperature of 32.4°C can easily be seen. Above this temperature, [[thenardite]] is the thermodynamically stable phase, while [[mirabilite]] is the stable phase below it, and this is differentiated by the dashed-lines. Other dashed or dot lines reflect the phase limits for the [[Sodium sulfate heptahydrate | sodium sulfate-heptahydrate]] as well as the phase III anhydrous sodium sulfate. These lines are the main difference to the previously shown diagrams. They represent metastable phases or regions. This means that these phases are not thermodynamically stable, but they can still form depending on the reaction kinetics. Although [[thenardite]] or [[mirabilite]] are the | |||
thermodynamically stable phases, the metastable heptahydrate and phase III can form depending on cooling or evaporation of the solutions and their possible formation should not be forgotten (for example,<bib id="Espinosa.etal:2008"/><bib id="Genkinger.etal:2007"/><bib id="Grossi.etal:2013"/><bib id="Linnow.etal:2006"/><bib id="Xu.etal:1999"/>). | |||
[[File:Na2SO4 Phasendiagramm.jpg|400px|thumb|left|''' | [[File:Na2SO4 Phasendiagramm.jpg|400px|thumb|left|'''Figure 4''': Phase diagram of the system Na<sup>+</sup>-SO<sub>4</sub><sup>2-</sup>-H<sub>2</sub>O. The water activity <i>a</i><sub>w</sub> is plotted versus temperature ''T''. <bib id="Steiger.etal:2008"/>]] | ||
<br clear=all> | <br clear=all> | ||
With regards to highly hygroscopic salts, such as [[Calcium nitrate | calcium nitrate]] or [[calcium chloride]] their phase diagrams do not show conditions for the formation of metastable phases, however, they are relevant. The equilibrium border between solution and crystallized salt provides the point at which the salt should crystallize out from the saturated solution; however, these saturated salt solutions may become supersaturated and therefore the solution will be below the DHR as a metastable solution <bib id="Steiger:2009a"/>. | |||
==Salt mixtures== | ==Salt mixtures== | ||
In | In most objects of cultural heritage mixtures of various ions, and therefore various salts, can be found, complicating the problem. It is not as easy to foretell their behaviour under given climatic conditions as it is for single salts, where the deliquescence humidity (DRH) and hydration equilibrium can be determined from the phase diagram. The various salts in the mixture influence their respective solubilities, so that their characteristic saturation RH are not the same. Thus, it is impossible to determine at what specific temperature the salt will start to deliquesce. For salt mixtures, rather than a single point there will be a temperature range for which the various phases can crystallize out of the mixtures. The influence of other salts on a specific one such as M<sub><i>ν</i>,M</sub>X<sub><i>ν</i>,X</sub>∙<i>n</i>H<sub>2</sub>O<i>ν</i>,can be given according to the thermodynamic solubility product (Eq. 2). A second salt that contains one of the ions of the first one will also influence its solubility (<i>m</i><sub>M</sub> or <i>m</i><sub>X</sub> may change), an even if this does not happen, nonetheless will <i>γ</i><sub>M</sub> and <i>γ</i>n<sub>X</sub> be influenced <bib id="Steiger.etal:2014"/>. An example for a mixture of two salts, where both have one ion in common is given below. | ||
As an example of a same ion salt mixture, the system KCl-NaCl-H<sub>2</sub>O will be considered. The diagram in Fig. 5 shows the molality of KCl with respect to that of NaCl. Because both salts contain chloride ions, the <i>m</i><sub>X</sub> of the salts be influenced (see Eq. 1). If the concentration of the second salt increases, so will the chloride concentration in the mixture, and this will reduce the solubility of the first salt. In a solution with the composition marked as A in the diagram, if water evaporates the solution will concentrate following the AB line. At point B, saturation with regards to KCl would be achieved, so that this salt would crystallize out. If evaporation continues, the crystallization of [[Sylvite |potassium chloride]] will modify further the composition of the solution, and the crystallization process will continue at point C; KCl will crystallize along its solubility curve, so that the potassium concentration decreases, while the [[ Halite |sodium chloride]] concentration increases. The crystallization end point C is reached when the saturation is attained also for NaCl, so that further evaporation leads to crystallization of both phases and drying out of the solution <bib id="Steiger:2009a"/>. | |||
[[File:KCl-NaCl mix.jpg|400px|thumb|left|'''Figure 5''': Solubility diagram of the system KCl-NaCl-H<sub>2</sub>O at 20 °C. The molality <i>m</i> of KCl is plotted versus <i>m</i> of NaCl <bib id="Steiger:2009a"/>.]] | |||
[[File:KCl-NaCl mix.jpg|400px|thumb|left|''' | |||
<br clear=all> | <br clear=all> | ||
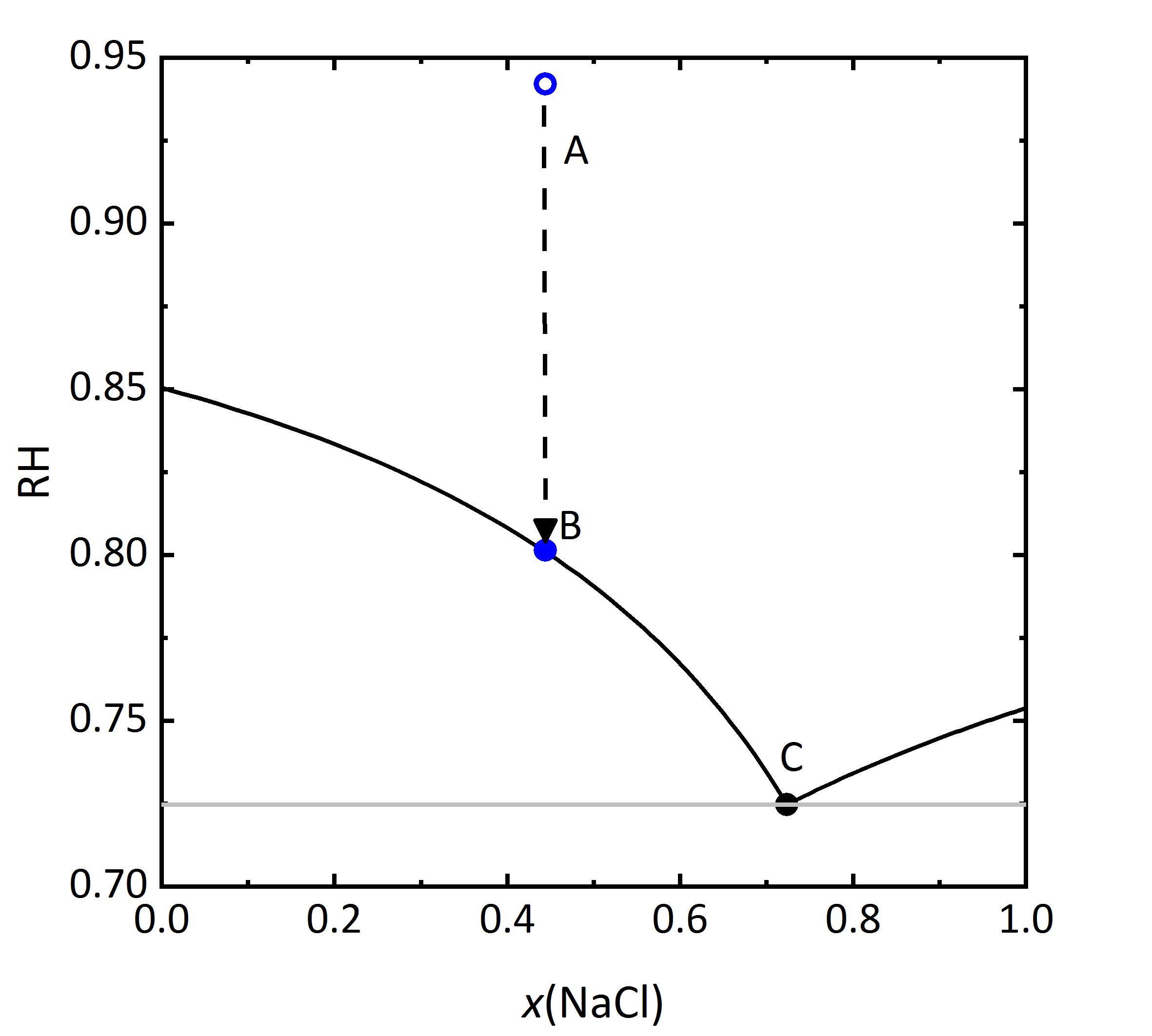
The diagram shown in Fig. 6 plots the RH as a function of the composition of the solution, where it can be seen that the saturation RH is also influenced when the salt is in a mixture; the equilibrium RH of the saturated solutions are also indicated. The composition, i.e., concentration of the solution is given in Mole-fraction of [[Halite | sodium chloride]] in relation to the mixture of all components. For lower concentrations, the amount of [[Sylvite |potassium chloride]] will be more important, by a 0.5 mixture, the same molal concentration for potassium and [[Halite | sodium chloride]] will be found. Point A in the diagram reflects a specific composition that has a specific RH that for this solution corresponds to 94.2% RH. Should the solution evaporate, the saturation point B will be reached, which corresponds to the saturation with respect to KCl, corresponding to 80.1% RH. The DRH of KCl by itself corresponds to 85% RH at 20ºC, so that when in a mixture, the crystallization of this salt will only occur at lower RH. This point could also be considered the equilibrium moisture, but is also the saturation moisture for point B. If the RH continues to decrease, when it reaches the 72.5% RH the final crystallization point will be reached. Similarly to points A, B, and C, if one starts with a concentration of [[Halite | sodium chloride]] >0.73 it can be seen that in this case the crystallization will start with [[Halite | sodium chloride]] at lower humidity than the DRH of the single salt. The diagram also shows that a single (critical) value at which the salt crystallizes is not sufficient in the case of mixtures. Rather, a range of relative humidity must be considered, where the crystallization process will be continuous <bib id="Steiger.etal:1996"/><bib id="Price.etal:1994"/><bib id="Steiger.etal:1995"/>. The upper limit of this area will be defined by the original composition of the mixture. The lower RH limit corresponds to the final crystallization point, when both phases will be present in the crystallized material. The value of this lower limit has also been referred to as <i>mutual deliquescence humidity</i> or MDRH, as it gives the RH value at which a mixed salt solution is in equilibrium with the crystalline salts <bib id="Steiger.etal:2014"/>. | |||
[[File:KCl-NaCl mix RH.jpg|400px|thumb|left|''' | [[File:KCl-NaCl mix RH.jpg|400px|thumb|left|'''Figure 6''': Saturation humidity at 20 °C for the system KCl-NaCl-H<sub>2</sub>O. The relative humidity is plotted versus mole fraction <i>x</i> of NaCl.]] | ||
<br clear=all> | <br clear=all> | ||
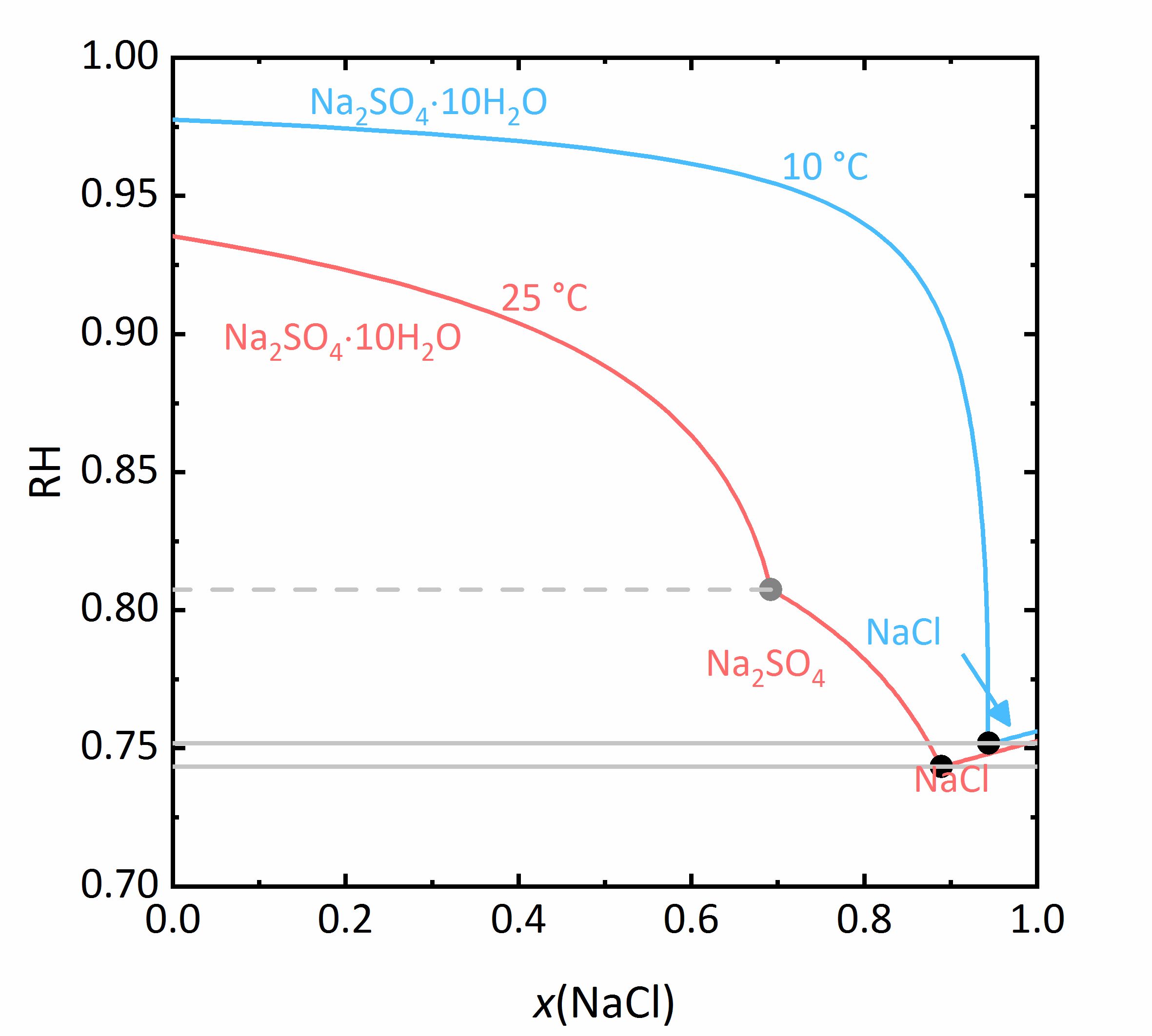
The next example shows a more complicated behaviour of salt mixtures in which there may be a salt that crystallizes in two or more degrees of hydration. In this case, the activity coefficient will be influenced as well as the water activity. For example, Fig. 7 shows a mixture of NaCl-Na<sub>2</sub>SO<sub>4</sub>-H<sub>2</sub>O. It can be seen that the solubility of [[mirabilite]] to which a high concentration of [[Halite | sodium chloride]] was added increases although the cation is the same. Since the water activity of the solution decreases with increasing concentration (i.e., evaporation of water), the solubility of the hydrated salt increases after a short initial decrease such as shown in the solubility diagram (Fig. 4) at 10ºC. The dehydration equilibrium for the system [[thenardite]]-[[mirabilite]] is highly dependent on the temperature as well as on the water activity. At temperatures below 18ºC, this dehydration will not occur, since the RH for the dehydration (grey line in the phase diagram of Na<sub>2</sub>SO<sub>4</sub> in Fig. 4, and for the mixture at 25ºC the grey dashed line in Figure 8) falls below the deliquescence humidity of the mixture. Only when the equilibrium moisture of the reaction is higher than the deliquescence humidity can dehydration or rehydration occur in the presence of the solution. Since there is a correlation between the water activity and the dehydration equilibrium, for example, the dehydration of [[mirabilite]] in the presence of other salts can occur at lower temperatures, even though [[thenardite]] in a Na<sup>+</sup>-SO<sub>4</sub><sup>2-</sup>-H<sub>2</sub>O system, would not be thermodynamically stable. This is an important consideration for the case of real situations, since hydration in the presence of a solution will be easier and faster compared to those occurring when only water vapor is present, thus accelerating the deterioration of materials. This issue is more relevant for more hygroscopic salt mixtures, since the deliquescence moisture of the mixture will have smaller values and the equilibrium moisture of the [[mirabilite]]-[[thenardite]]-conversion will be exceeded more often. It is to be considered, that the values of the equilibrium moisture for this transformation are not influenced by other salts. A decisive point is whether the values of the transformation falls above or below the deliquescence humidity of the mixture <bib id="Steiger.etal:2014"/>. | |||
[[File:NaCl-Na2SO4 mix.jpg|400px|thumb|left|''' | [[File:NaCl-Na2SO4 mix.jpg|400px|thumb|left|'''Figure 7''': Solubilities in the system NaCl-Na<sub>2</sub>SO<sub>4</sub>-H<sub>2</sub>O at 25 °C (red) and 10 °C (blue). The molality <i>m</i> of Na<sub>2</sub>SO<sub>4</sub> is plotted versus <i>m</i> of NaCl <bib id="Steiger.etal:2014"/>.]] | ||
<br clear=all> | <br clear=all> | ||
[[File:NaCl Na2SO4 mix RH.jpg|400px|thumb|left|''' | [[File:NaCl Na2SO4 mix RH.jpg|400px|thumb|left|'''Figure 8''': Saturation humidities at 25°C (red) and at 10 °C (blue) for the system NaCl-Na<sub>2</sub>SO<sub>4</sub>-H<sub>2</sub>O. The relative humidity is plotted versus the mole fraction <i>x</i> of NaCl.]] | ||
<br clear=all> | <br clear=all> | ||
==Salt mixtures | ==Salt mixtures where a double salt may form== | ||
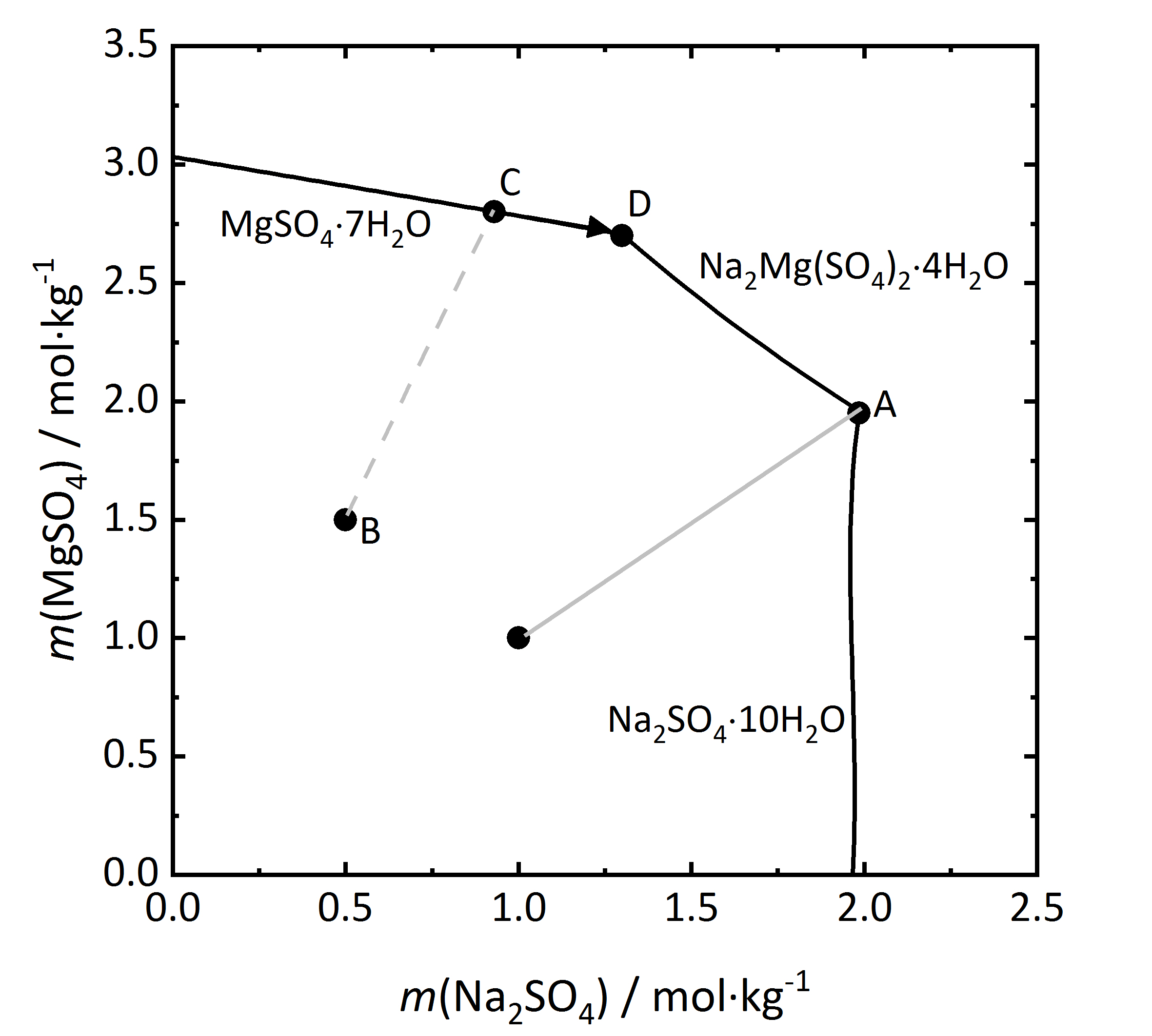
Further considerations on salt mixtures can be made, especially when double salts can form that may have three of more different ions. As previously mentioned, there are both congruent and incongruent soluble double salts. A solubility diagram for the mixture Na<sub>2</sub>SO<sub>4</sub> and MgSO<sub>4</sub> will be considered (Fig.9), since a congruent double salt [[astrakanite]], also referred to as [[Astrakanite | blödite]] can form Na<sub>2</sub>Mg(SO<sub>4</sub>)<sub>2</sub>∙4H<sub>2</sub>O. The concentration of both salts are shown for a 25ºC temperature (the phases Na<sub>2</sub>SO<sub>4</sub>∙10H<sub>2</sub>O and MgSO<sub>4</sub>∙7H<sub>2</sub>O are the stable phases at this temperature). Since the double salt has a congruent solubility, it will crystallize out of the solution, having the same composition as the salt itself. From the salt formula it can be seen that it is formed by and equimolar mixture of sodium and magnesium sulfate. This is shown in the diagram by the light grey line. When reaching the saturation concentration in point A, only astrakanite will crystallize out, behaving as if it were a single salt, although it is composed of equal amounts of sodium sulfate and magnesium sulfate. The deliquescence behaviour can be similarly considered. If only [[astrakanite]] is present, it will start to absorb water vapor from the environment once it passes it staturation moisture and forming a saturated solution. If the RH continues to rise, it will result in an equimolar solution of sodium and magnesium sulfate <bib id="Steiger.etal:2014"/>. However if a mixture that has more magnesium sulfate (point B) in the diagram, then by evaporation of the solution the [[Epsomite | magnesium sulfate heptahydrate]] will crystallize out (point C), and the crystalization continues then along the C-D line. At this point D, because of the increasing content of [[sodium sulfate], [[astrakanite]] will crystallize out, ending the crystallization process. | |||
[[File:Na2SO4-MgSO4 mix.jpg|400px|thumb|left|''' | |||
[[File:Na2SO4-MgSO4 mix.jpg|400px|thumb|left|'''Figure 9''': Solubilities at 25 °C for the system Na<sub>2</sub>SO<sub>4</sub>-MgSO<sub>4</sub>-H<sub>2</sub>O. The molality <i>m</i> of MgSO<sub>4</sub> is plotted versus <i>m</i> of Na<sub>2</sub>SO<sub>4</sub> <bib id="Steiger.etal:2014"/>.]] | |||
<br clear=all> | <br clear=all> | ||
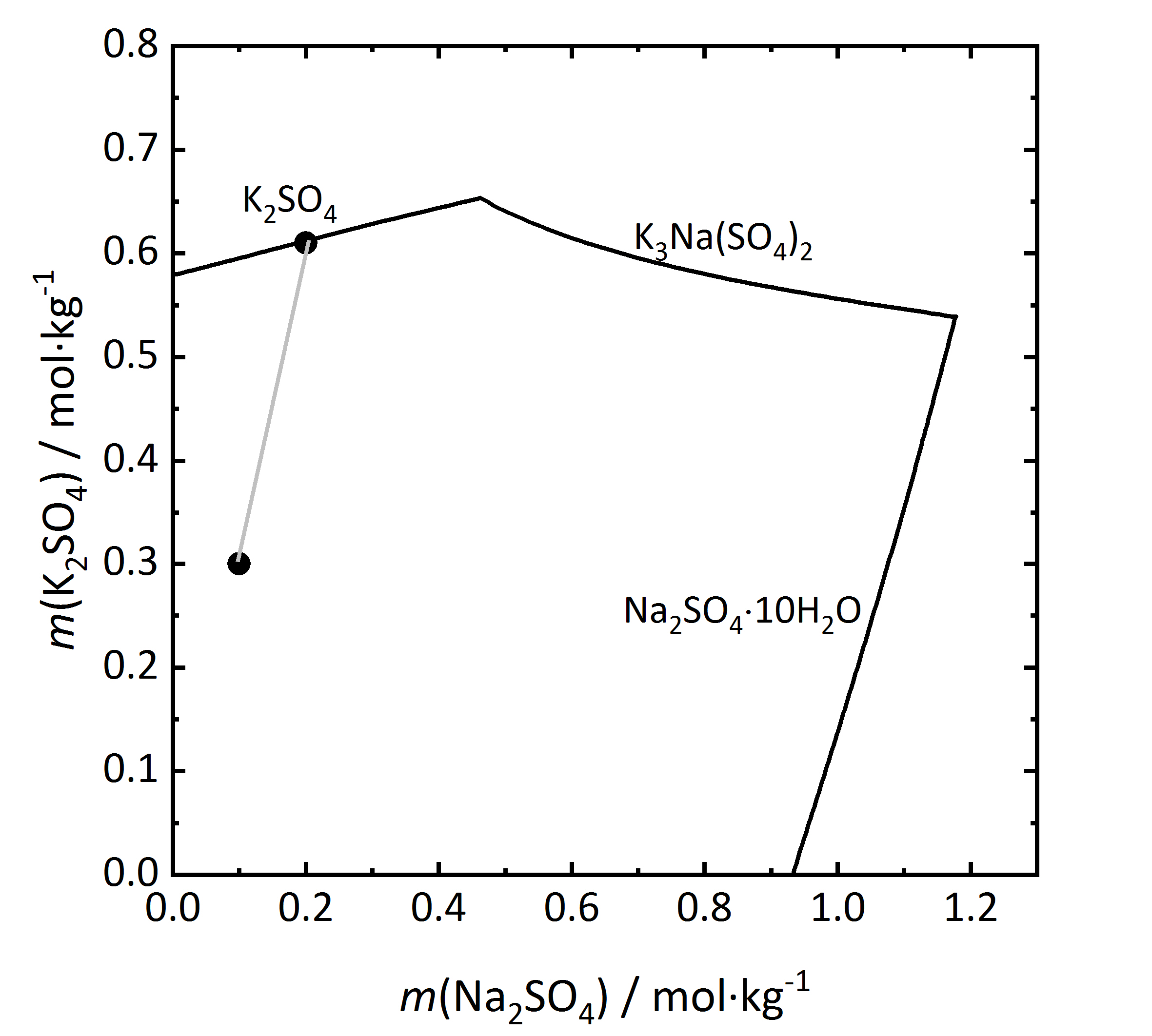
The solubility diagram of an incongruent double salt is shown in Fig. 10. [[Aphthitalite]] (K<sub>3</sub>Na(SO<sub>4</sub>)<sub>2</sub>) is constituted by a 3:1 mixture (in terms of molality) of potassium and sodium sulfate. By evaporation of a solution with this composition at 15ºC it can be seen that [[Arcanite | potassium sulfate]] will crystallize as [[arcanite]], not as [[aphthitalite]], since from the composition of the double salt, saturation is found only with regards to [[arcanite]]. Dissolution of [[aphthitalite]] in water will not result in a saturated solution, since [[arcanite]] would crystallize out <bib id="Steiger.etal:2014"/>. | |||
[[File:K2SO4-Na2SO4 mix.jpg|400px|thumb|left|''' | [[File:K2SO4-Na2SO4 mix.jpg|400px|thumb|left|'''Figure 10''': Solubilities at 15 °C for the system K<sub>2</sub>SO<sub>4</sub>-Na<sub>2</sub>SO<sub>4</sub>-H<sub>2</sub>O. The molality <i>m</i> of K<sub>2</sub>SO<sub>4</sub> is plotted versus <i>m</i> of Na<sub>2</sub>SO<sub>4</sub> <bib id="Steiger.etal:2014"/>.]] | ||
<br clear=all> | <br clear=all> | ||
So far, only salt mixtures with three different ions were considered. The behaviour and the representation of mixtures with four different ions is far more complicated. | |||
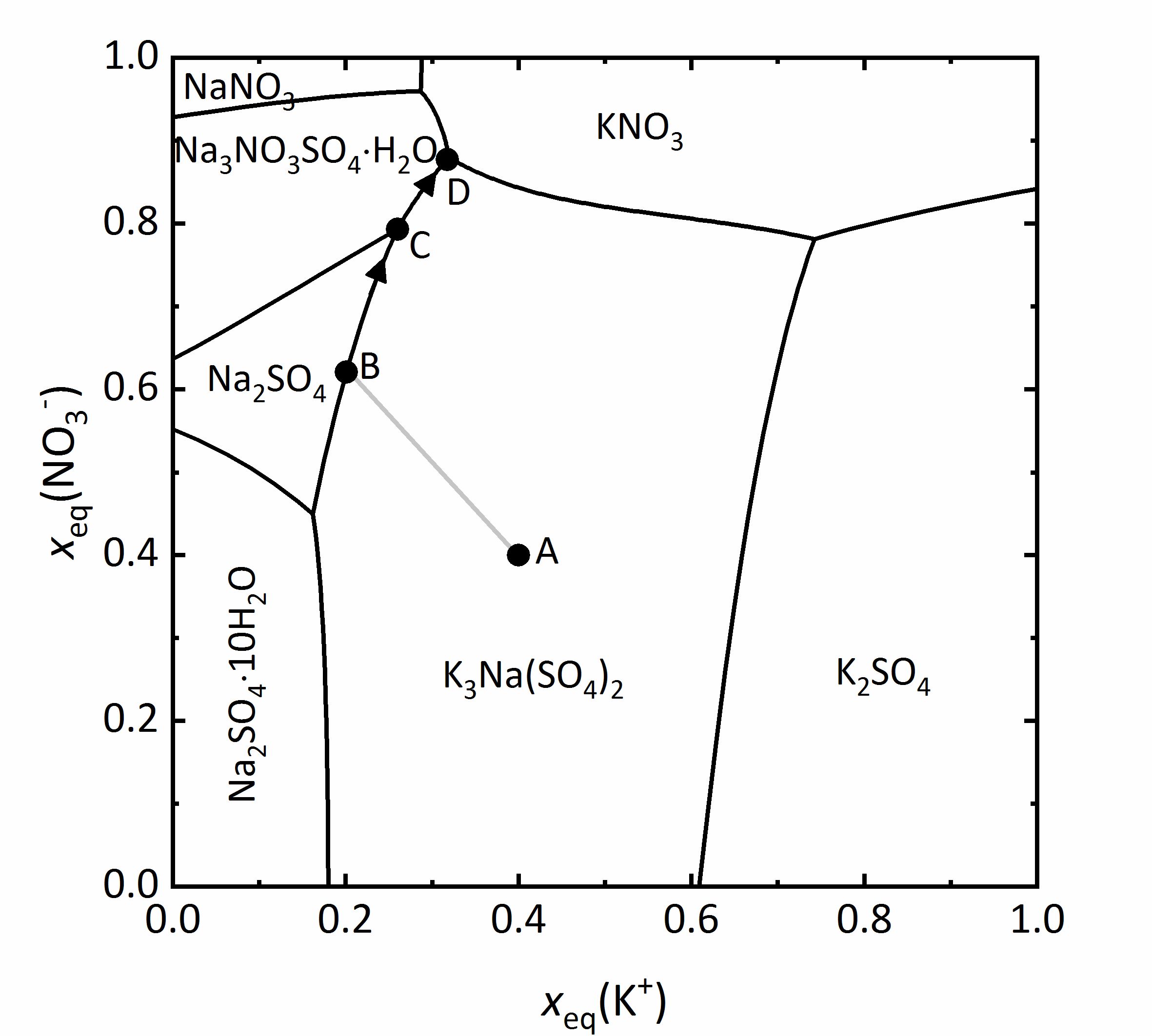
The representation can be simplified by not including water as a component. This type of representation is referred also as a Jänecke-projection <bib id="Jaenecke:1906"/>. An example of this type of diagram is given for the mixture of Na<sup>+</sup>-K<sup>+</sup>-NO<sub>3</sub><sup>-</sup>-SO<sub>4</sub><sup>2-</sup>-H<sub>2</sub>O at 25ºC (Fig. 11). The ordinate axis shows the mole fractions of the equivalent charges of the nitrate ions, the abscissa shows that corresponding to the potassium ions. All mixtures are presented by the charge equivalent mole fraction, so that the value of the ions is taken into account. In this diagram this means that various mixtures appear as partial contribution of the potassium cations or nitrate anions relative to the total amount of positive or negative charges. For example, it is clear that the amount of potassium and nitrate ions outweigh the sodium and sulfate ions at very low molar ratios. Therefore, in the four corners of the diagram are the pure four salts: at the bottom left [[sodium sulfate]]; top left [[Nitronatrite | sodium nitrate]], top right [[Niter | potassium nitrate]] and bottom right [[Arcanite | potassium sulfate.]] The areas within the diagram show the stability ranges for the possible phases. They are separated by lines, representing the saturation concentration of the solutions, which correspond to the adjacent in equilibrium. This means that in any such field, only a single phase is present, in points where more lines converge there are three phases in equilibrium. At these points there are isothermic invariant phases (phase rule) <bib id="Steiger.etal:2014"/>. | |||
As an example, a salt solution with a composition corresponding to point A falls in the stability area of [[Aphthitalite | glaserits]] (NaK<sub>3</sub>(SO<sub>4</sub>)<sub>2</sub>), so that this salt will crystallize out first upon evaporation of the solution. During crystallization and further evaporation, the composition of the solution will change following the line A-B. Once at point B, the saturation corresponds to [[thenardite]] and both salts will crystallize out. This modifies further the composition of the solution following the line B-C, reaching the area for the saturation of [[darapskite]] (Na<sub>3</sub>NO<sub>3</sub>SO<sub>4</sub>∙H<sub>2</sub>O). This is, however, and invariant point, so that only these three phases can appear together. By further evaporation of the solution, [[thenardite]] will dissolve, since its stability area does not include the C-D limit. Therefore, point D is where the final crystallization occurs <bib id="Steiger:2009a"/><bib id="Steiger.etal:2008c"/>. | |||
[[File:Na-K-SO4-NO3 mix.jpg|400px|thumb|left|'''Figure 11''': Solubilities at 25 °C in the system Na<sup>+</sup>-K<sup>+</sup>-NO<sub>3</sub><sup>-</sup>-SO<sub>4</sub><sup>2-</sup>-H<sub>2</sub>O. The charge equivalent mole fraction <i>x</i><sub>eq</sub> of NO<sub>3</sub><sup>-</sup> is plotted versus <i>x</i><sub>eq</sub> of K<sup>+</sup> <bib id="Steiger:2009a"/>, calculated according to <bib id="Steiger.etal:2008c"/>.]] | |||
<br clear=all> | |||
The phase diagrams are important to show how the crystallization will proceed, as well as being practically useful because the size of the stability fields of the various phases gives an idea as to how probable it is that a particular phase will crystallize. The larger the field, the more compositions can lead to the same phase. Furthermore, it is important to know which phases can be found together: only those phases having a common limiting line or those that form at an invariant point. In the example given, it would be impossible to find [[mirabilite]] together with [[Niter | potassium nitrate]] or [[Arcanite | potassium sulfate]] <bib id="Steiger.etal:2014"/>. | |||
==Literature== | ==Literature== | ||
| Line 130: | Line 131: | ||
<biblist/> | <biblist/> | ||
[[ | [[Category:Salt]] [[Category:Stahlbuhk,Amelie]] [[Category:R-MSteiger]] | ||
Latest revision as of 16:08, 29 March 2023
Author: Amelie Stahlbuhk
back to Saltwiki:Community portal
Abstract[edit]
The key properties of salts and salt mixtures are described by means of phase and solubility diagrams. Mainly those salts relevant to cultural heritage objects are addressed.
Salts in cultural heritage objects[edit]
Salts are based on ionic compounds, having both positively charged ions (cations) and a negatively charged ions (anions). Both cations and anions can have one or more positive or negative charges but they must balance out in the salt. Cultural heritage objects of porous, inorganic materials, such as buildings monuments, may be contaminated with salts. The most common cations are sodium (Na+), potassium (K+), magnesium (Mg++) and calcium (Ca++). For the case of anions, the most frequently found are chloride (Cl-), sulfate (SO4=), nitrate (NO3-)and carbonate (CO3=). Depending on the environment of the object, origin of the salts and past restorations/conservation measure, there may be other cations present, such as barium (Ba++) or ammonium (NH4+), or anions, such as acetate (CH3COO-). The latter one is particularly relevant in the case where objects, such as ceramics, are displayed or stored in wooden cases which emit acetic acid over time, resulting in the efflorescence of an acetate salt, such as sodium or potassium from the object itself. In the case of metal objects, other cations may also appear. The following section will focus mainly on the most common minerals.
Single, double or triple salt[edit]
Salts can be differentiated depending on the number of cations or anions they contain. If there is only one cation and one anion, such as in sodium chloride NaCl, then it is a single salt. An example of a double salt could be that of darapskite, which contains only one cation, sodium, but two different anions, sulfate and nitrate (Na3(SO4)(NO3)∙H2O) as well as aphtitalite, which has two cations sodium and potassium, but only one anion, sulfate (K3Na(SO4)2). However, this formula could also be written as follows: Na2SO4∙3K2SO4 or (K3Na(SO4)2), the former showing that the salt is actually composed by a combination of two single salts.
Some double salts may be found on building materials, these may form depending on environmental conditions, as well as triple salts; the latter, according to the definition may have three different cations or anions, however, these are not found as frequently.
In the case of double salts, some may differentiate themselves depending on whether they have a congruent or incongruent solubility. In the case of a congruent solubility, when the salt dissolves in water, the solution will have the same mixture of anions and cations as the salt itself, and when it evaporates, the same salt will precipitate out. In the case of incongruent solubility, depending on the concentration of the produced solution, other phases may crystallize out, so that the solution will no longer have the same composition as the original salt, therefore, when the solution evaporates completely, the original salt will not necessarily be obtained, since some phases had separated previously. The crystallization and dissolution processes of incongruent salts is very complex and information regarding their solubility and crystallization processes is not easily predictable.
Salt solubility[edit]
Salts have distinct solubilities that are temperature dependent. For buildings contaminated by salts this is an important point, since the mobility of a particular salt will depend on its solubility: those with lower solubility will crystallize sooner. Considering a wall with rising damp, where the ground water and the salts it contains, rises by capillarity, a fractionation of the salts can be detected. Salts with low solubility will crystallize out close to where the water enters the wall, while highly soluble salts may rise higher [Arnold.etal:1991]Title: Monitoring Wall Paintings Affected by soluble Salts
Author: Arnold, Andreas; Zehnder, Konrad .
.
The solubility temperature dependence can be described by solubility diagrams. To illustrate the point the solubility diagram for a single salt, such as potassium nitrate, is shown in Fig. 1. In this diagram, the solubility of the salt in water is given by its concentration expressed in molality (mol/kgsolvent, where the solvent is water) on the ordinate axis as a function of temperature on the abscissa axis. The black line in the diagram reflects the saturation concentration of the salt as a function of the temperature. At 20°C, the solution of the potassium nitrate would have a molality of 3.1 mol/kg corresponding to a saturated solution. Below the line, the solution is not saturated, above the line the solution is saturated and salt will precipitate out. In the case of this salt, the solubility increases with temperature. At very low temperatures, ice will also crystallize out.
For a given salt, the equilibrium between crystallization and dissolution can be described by the following equation:
Mν,MXν,X•ν0H2O ⇌ νMMzM++νXXzX-+ν0H2O (Eq. 1)
M and X are the cations and anions with their number ν and their charge z while ν0 represents the number of possible water molecules, so that the equation can also be applied to hydrated salts. The corresponding equilibrium constant is the solubility product lnKMX.
lnKMX=νMlnmM+νXlnmX+νMlnγM+νXlnγX+ν0lnaw (Eq. 2)
The molalities are m and the activation coefficient of the cations and anions in a saturated solution of the salt is given by γ while the water activity is given by aw.
aw=RH=pw/pw,0 (Eq. 3)
In the above, the actual water vapor partial pressure is given by pw and the saturation partial pressure is given by pw,0, so that the water activity of a solution in equilibrium equals the air moisture above the solution.
Hydrated salts[edit]
Some salts may crystallize both as anhydrous as well as hydrated phases with one or more water molecules, the latter being embedded into the crystal structure. Mirabilite, Na2SO4∙10H2O forms from the system Na+-SO42--H2O and crystallizes with ten water molecules inserted in the crystal, with a ratio of one mole Na2SO4 to ten moles H2O. A hydration reaction can be postulated similarly to a solubility reaction:
Mν,MXν,X•ν0,AH2O+(ν0,B-ν0,A)H2O(g) ⇌ Mν,MXν,X•ν0,BH2O (Eq. 4)
where ν0,A corresponds to the number of water molecules in the lower hydration phase and ν0,B corresponding to the higher hydration phase. The equilibrium constant for the hydration reaction KH can be formulated as follows:
KH=pw0/pw,AB=1/RHAB (Eq. 5)
The saturation partial pressure, or deliquescence, pw0 is related to the water vapor pressure corresponding to the equilibrium between the lower (A) and the higher (B) hydration phase pw,AB, resulting in the reciprocal value of the relative humidity (RH) in equilibrium with both phases, A and B, RHAB. When the RH increases above that for RHAB hydration of the salt will occur, while if the RH decreases below that value, dehydration will occur. [Steiger.etal:2014]Title: Weathering and Deterioration
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja [Steiger:2009a]Title: Modellierung von Phasengleichgewichten
[Steiger:2009a]Title: Modellierung von Phasengleichgewichten
Author: Steiger, Michael .
.
Phase diagrams[edit]
Salts with the general formula Mz+-Xz--H2O (where M corresponds to the cations, and X to the anions, where several ions can be included, some having different charges z) can result in the formation of different phases depending on the temperature and relative humidity (RH). From the phase diagrams the stability conditions for the various phases can be determined.
For the case of single salts that do not hydrate there is a specific relation between temperature and RH above which the salt will begin to absorb water vapor from the air to form a saturated solution. This point is defined as the deliquescence relative humidity (DRH), where the crystalline phase, the saturated solution and the water vapor above it are in equilibrium thus corresponding to the water activity of the solution. In the phase diagram for sodium nitrate shown in (Fig. 2) it can be seen that the DRH at a temperature of 20°C corresponds to 75.3 % RH. The diagram also shows that the DRH will decrease with increasing temperature. Above the line corresponding to the saturated salt solution, it can be seen that with increasing RH and at a given temperature the ongoing water vapor absorption will dilute the solution. On the other hand, with decreasing RH, the solution will concentrate as water vapor is released into the environment, until the salt reprecipitates upon reaching the DRH value. How much water will be absorbed above the DRH depends on the equilibrium between solution and water vapor in the environment, i.e., RH. In equilibrium, the water activity of the solution will correspond to the RH of the environment (Eq. 3). If humidity rises, the system will absorb more water vapor from the environment so that equilibrium is restored.
Author: Steiger, Michael; Kiekbusch, Jana; Nicolai, Andreas

Apart from single salts, there are many salts which may have different hydrated phases. A relatively simple phase diagram to illustrate such a system is that corresponding to Ca2+-NO3--H2O (Fig. 3). In this case, three different hydration phases can be found apart from the anhydrous one. Similarly to the DRH that reflects the point where the salt will start to absorb water vapor to form a saturated solution, there is in this case a RH value where the anhydrous salt will absorb water to form a hydrated phase, and if more hydration phases can form, there will be several points. The phase diagram shows the different hydration phases that the salt can form. Different lines will show their stability areas. The different DRH for the hydrates are shown by the thicker drawn lines, and they describe the equilibrium between the crystalline salt, the saturated solution and the water vapor in the air. There are also other thinner lines that describe the phase changes between the various hydration-dehydration equilibria between the lower and higher hydration phases. It is also important to consider the formation of ice, which is shown by the dotted line. Thus, at temperatures below 0°C, the equilibrium with ice needs also to be considered together with that of the tetrahydrate calcium nitrate (nitrocalcite) [Steiger.etal:2014]Title: Weathering and Deterioration
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
Phase diagrams for salts having several hydrates can be even more complex, so another example will be given for the system
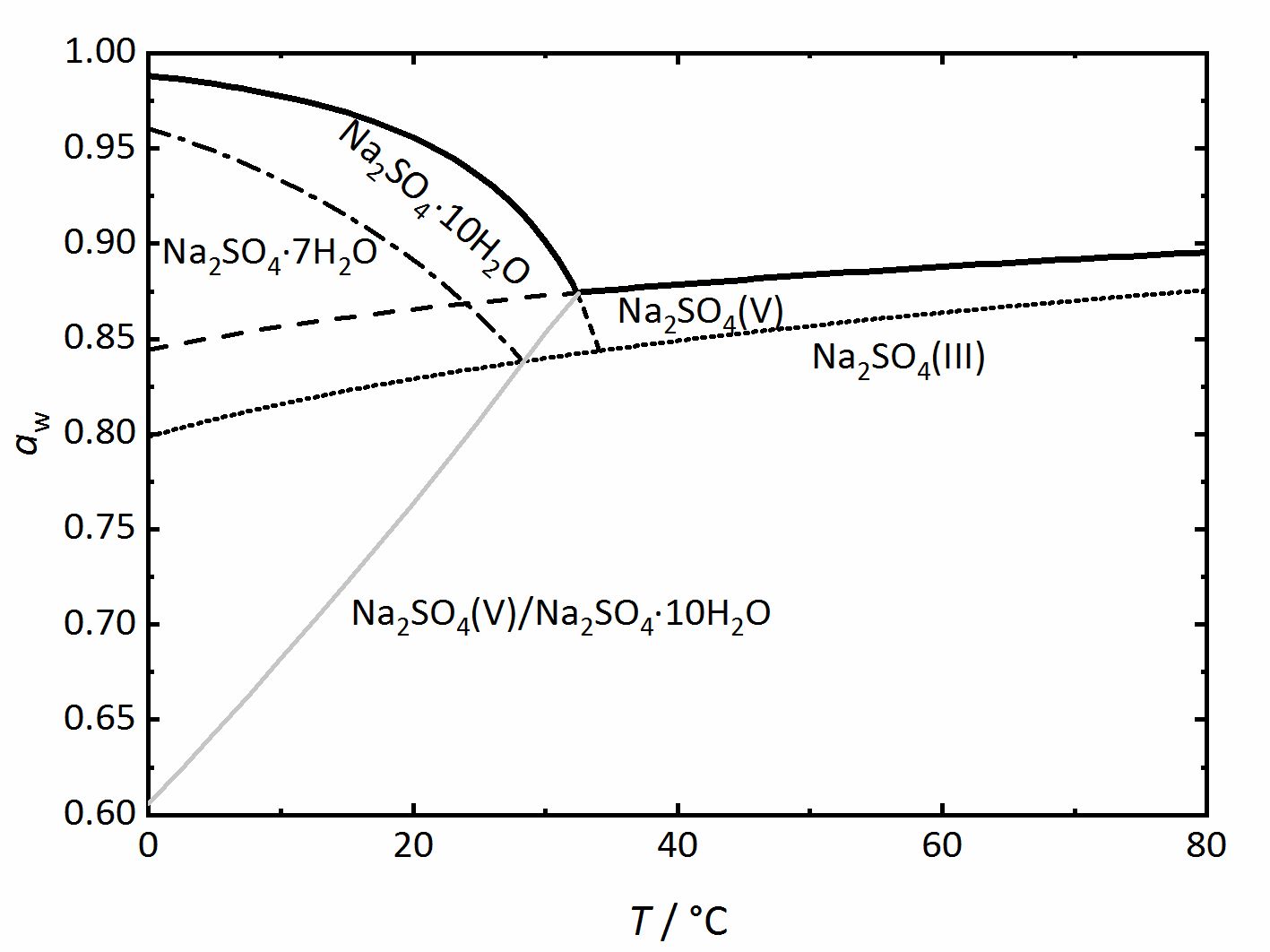
Na+-SO42--H2O [Steiger.etal:2008]Title: Crystallization of sodium sulfate phases in porous materials: The phase diagram Na2SO4–H2O and the generation of stress
Author: Steiger, Michael; Asmussen, Sönke (Fig. 4). Again, thicker lines show the equilibrium between the saturated solution and the crystalline phase in question, corresponding to the DRH value. They grey line represents the dehydration or the hydration equilibrium between the anhydrous phase (thenardite) and the decahydrate (mirabilite). Mirabilite and thenardite are not stable at all temperatures, so that the transition temperature of 32.4°C can easily be seen. Above this temperature, thenardite is the thermodynamically stable phase, while mirabilite is the stable phase below it, and this is differentiated by the dashed-lines. Other dashed or dot lines reflect the phase limits for the sodium sulfate-heptahydrate as well as the phase III anhydrous sodium sulfate. These lines are the main difference to the previously shown diagrams. They represent metastable phases or regions. This means that these phases are not thermodynamically stable, but they can still form depending on the reaction kinetics. Although thenardite or mirabilite are the
thermodynamically stable phases, the metastable heptahydrate and phase III can form depending on cooling or evaporation of the solutions and their possible formation should not be forgotten (for example,[Espinosa.etal:2008]Title: Model for the mechanical stress due to the salt crystallization in porous materials
(Fig. 4). Again, thicker lines show the equilibrium between the saturated solution and the crystalline phase in question, corresponding to the DRH value. They grey line represents the dehydration or the hydration equilibrium between the anhydrous phase (thenardite) and the decahydrate (mirabilite). Mirabilite and thenardite are not stable at all temperatures, so that the transition temperature of 32.4°C can easily be seen. Above this temperature, thenardite is the thermodynamically stable phase, while mirabilite is the stable phase below it, and this is differentiated by the dashed-lines. Other dashed or dot lines reflect the phase limits for the sodium sulfate-heptahydrate as well as the phase III anhydrous sodium sulfate. These lines are the main difference to the previously shown diagrams. They represent metastable phases or regions. This means that these phases are not thermodynamically stable, but they can still form depending on the reaction kinetics. Although thenardite or mirabilite are the
thermodynamically stable phases, the metastable heptahydrate and phase III can form depending on cooling or evaporation of the solutions and their possible formation should not be forgotten (for example,[Espinosa.etal:2008]Title: Model for the mechanical stress due to the salt crystallization in porous materials
Author: Espinosa, R.; Franke, L.; Deckelmann, G. [Genkinger.etal:2007]Title: Crystallisation of sodium sulfate: supersaturation and metastable phases
[Genkinger.etal:2007]Title: Crystallisation of sodium sulfate: supersaturation and metastable phases
Author: Genkinger, Selma; Putnis, Andrew [Grossi.etal:2013]Title: Acoustic emission monitoring to study sodium sulphate crystallization in monumental porous carbonate stones
[Grossi.etal:2013]Title: Acoustic emission monitoring to study sodium sulphate crystallization in monumental porous carbonate stones
Author: Grossi, C.M.; Esbert, R.M.; Suarez del Rio, L.M.; Montoto, M.; Laurenzi-Tabasso, M. [Linnow.etal:2006]Title: Investigation of Sodium Sulfate Phase Transitions in a Porous Material Using Humidity- and Temperature-Controlled X-ray Diffraction
[Linnow.etal:2006]Title: Investigation of Sodium Sulfate Phase Transitions in a Porous Material Using Humidity- and Temperature-Controlled X-ray Diffraction
Author: Linnow, Kirsten; Zeunert, Anke; Steiger, Michael [Xu.etal:1999]Title: In-situ Raman observations of phase transformation of Na2SO4 during the hydration/dehydration cycles on single levitated microparticle.
[Xu.etal:1999]Title: In-situ Raman observations of phase transformation of Na2SO4 during the hydration/dehydration cycles on single levitated microparticle.
Author: Xu B., Schweiger G. ).
).
Author: Steiger, Michael; Asmussen, Sönke

With regards to highly hygroscopic salts, such as calcium nitrate or calcium chloride their phase diagrams do not show conditions for the formation of metastable phases, however, they are relevant. The equilibrium border between solution and crystallized salt provides the point at which the salt should crystallize out from the saturated solution; however, these saturated salt solutions may become supersaturated and therefore the solution will be below the DHR as a metastable solution [Steiger:2009a]Title: Modellierung von Phasengleichgewichten
Author: Steiger, Michael .
.
Salt mixtures[edit]
In most objects of cultural heritage mixtures of various ions, and therefore various salts, can be found, complicating the problem. It is not as easy to foretell their behaviour under given climatic conditions as it is for single salts, where the deliquescence humidity (DRH) and hydration equilibrium can be determined from the phase diagram. The various salts in the mixture influence their respective solubilities, so that their characteristic saturation RH are not the same. Thus, it is impossible to determine at what specific temperature the salt will start to deliquesce. For salt mixtures, rather than a single point there will be a temperature range for which the various phases can crystallize out of the mixtures. The influence of other salts on a specific one such as Mν,MXν,X∙nH2Oν,can be given according to the thermodynamic solubility product (Eq. 2). A second salt that contains one of the ions of the first one will also influence its solubility (mM or mX may change), an even if this does not happen, nonetheless will γM and γnX be influenced [Steiger.etal:2014]Title: Weathering and Deterioration
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja . An example for a mixture of two salts, where both have one ion in common is given below.
. An example for a mixture of two salts, where both have one ion in common is given below.
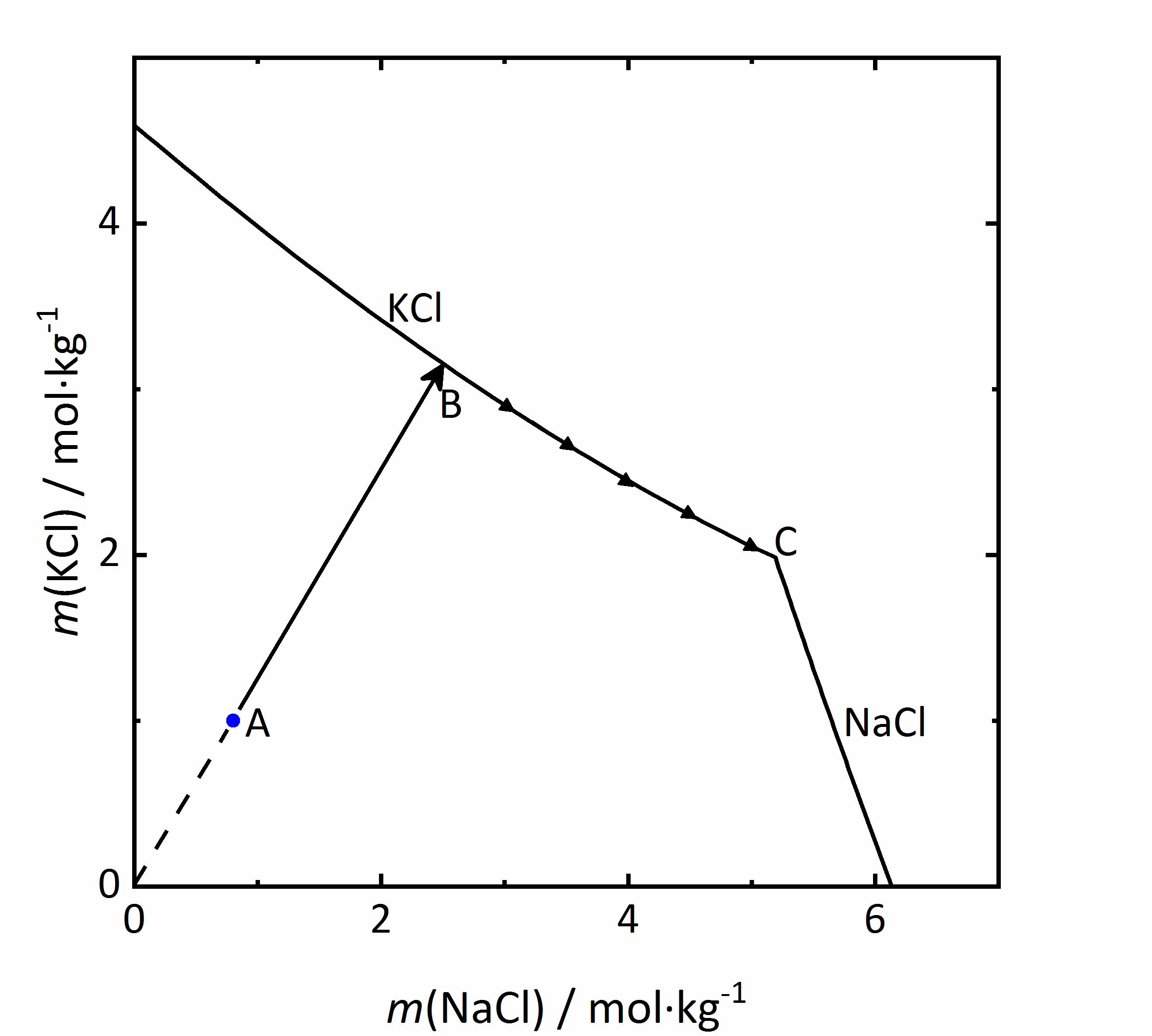
As an example of a same ion salt mixture, the system KCl-NaCl-H2O will be considered. The diagram in Fig. 5 shows the molality of KCl with respect to that of NaCl. Because both salts contain chloride ions, the mX of the salts be influenced (see Eq. 1). If the concentration of the second salt increases, so will the chloride concentration in the mixture, and this will reduce the solubility of the first salt. In a solution with the composition marked as A in the diagram, if water evaporates the solution will concentrate following the AB line. At point B, saturation with regards to KCl would be achieved, so that this salt would crystallize out. If evaporation continues, the crystallization of potassium chloride will modify further the composition of the solution, and the crystallization process will continue at point C; KCl will crystallize along its solubility curve, so that the potassium concentration decreases, while the sodium chloride concentration increases. The crystallization end point C is reached when the saturation is attained also for NaCl, so that further evaporation leads to crystallization of both phases and drying out of the solution [Steiger:2009a]Title: Modellierung von Phasengleichgewichten
Author: Steiger, Michael .
.
Author: Steiger, Michael
 .
.
The diagram shown in Fig. 6 plots the RH as a function of the composition of the solution, where it can be seen that the saturation RH is also influenced when the salt is in a mixture; the equilibrium RH of the saturated solutions are also indicated. The composition, i.e., concentration of the solution is given in Mole-fraction of sodium chloride in relation to the mixture of all components. For lower concentrations, the amount of potassium chloride will be more important, by a 0.5 mixture, the same molal concentration for potassium and sodium chloride will be found. Point A in the diagram reflects a specific composition that has a specific RH that for this solution corresponds to 94.2% RH. Should the solution evaporate, the saturation point B will be reached, which corresponds to the saturation with respect to KCl, corresponding to 80.1% RH. The DRH of KCl by itself corresponds to 85% RH at 20ºC, so that when in a mixture, the crystallization of this salt will only occur at lower RH. This point could also be considered the equilibrium moisture, but is also the saturation moisture for point B. If the RH continues to decrease, when it reaches the 72.5% RH the final crystallization point will be reached. Similarly to points A, B, and C, if one starts with a concentration of sodium chloride >0.73 it can be seen that in this case the crystallization will start with sodium chloride at lower humidity than the DRH of the single salt. The diagram also shows that a single (critical) value at which the salt crystallizes is not sufficient in the case of mixtures. Rather, a range of relative humidity must be considered, where the crystallization process will be continuous [Steiger.etal:1996]Title: Crystallization properties of salt mixtures: Comparison of experimental results and model calculations
Author: Steiger, Michael; Zeunert, Anke [Price.etal:1994]Title: Preventing salt damage in porous materials
[Price.etal:1994]Title: Preventing salt damage in porous materials
Author: Price, Clifford A.; Brimblecomb, Peter [Steiger.etal:1995]Title: Hygroskopische Eigenschaften und Kristallisationsverhalten von Salzgemischen
[Steiger.etal:1995]Title: Hygroskopische Eigenschaften und Kristallisationsverhalten von Salzgemischen
Author: Steiger, Michael; Dannecker, Walter . The upper limit of this area will be defined by the original composition of the mixture. The lower RH limit corresponds to the final crystallization point, when both phases will be present in the crystallized material. The value of this lower limit has also been referred to as mutual deliquescence humidity or MDRH, as it gives the RH value at which a mixed salt solution is in equilibrium with the crystalline salts [Steiger.etal:2014]Title: Weathering and Deterioration
. The upper limit of this area will be defined by the original composition of the mixture. The lower RH limit corresponds to the final crystallization point, when both phases will be present in the crystallized material. The value of this lower limit has also been referred to as mutual deliquescence humidity or MDRH, as it gives the RH value at which a mixed salt solution is in equilibrium with the crystalline salts [Steiger.etal:2014]Title: Weathering and Deterioration
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
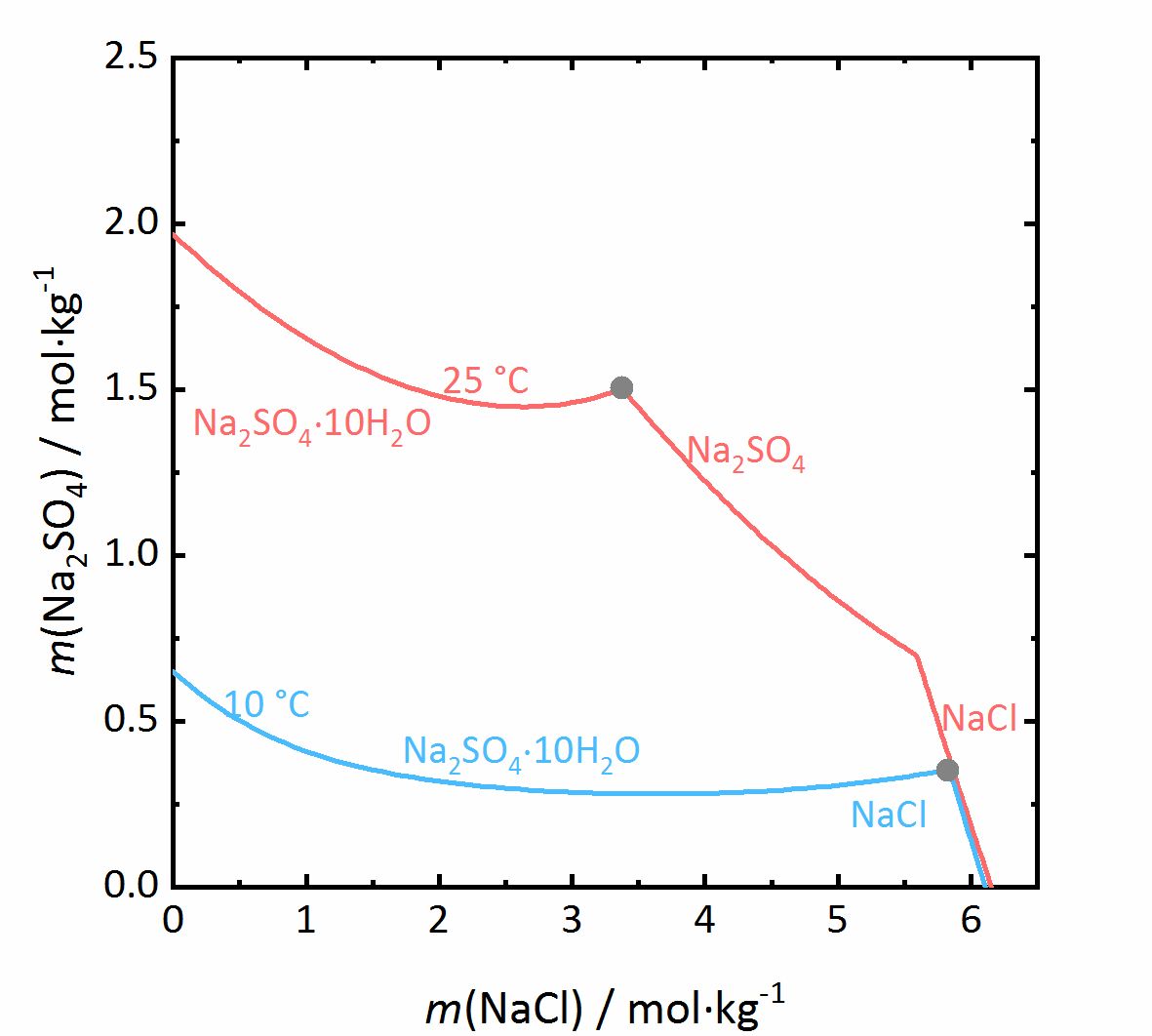
The next example shows a more complicated behaviour of salt mixtures in which there may be a salt that crystallizes in two or more degrees of hydration. In this case, the activity coefficient will be influenced as well as the water activity. For example, Fig. 7 shows a mixture of NaCl-Na2SO4-H2O. It can be seen that the solubility of mirabilite to which a high concentration of sodium chloride was added increases although the cation is the same. Since the water activity of the solution decreases with increasing concentration (i.e., evaporation of water), the solubility of the hydrated salt increases after a short initial decrease such as shown in the solubility diagram (Fig. 4) at 10ºC. The dehydration equilibrium for the system thenardite-mirabilite is highly dependent on the temperature as well as on the water activity. At temperatures below 18ºC, this dehydration will not occur, since the RH for the dehydration (grey line in the phase diagram of Na2SO4 in Fig. 4, and for the mixture at 25ºC the grey dashed line in Figure 8) falls below the deliquescence humidity of the mixture. Only when the equilibrium moisture of the reaction is higher than the deliquescence humidity can dehydration or rehydration occur in the presence of the solution. Since there is a correlation between the water activity and the dehydration equilibrium, for example, the dehydration of mirabilite in the presence of other salts can occur at lower temperatures, even though thenardite in a Na+-SO42--H2O system, would not be thermodynamically stable. This is an important consideration for the case of real situations, since hydration in the presence of a solution will be easier and faster compared to those occurring when only water vapor is present, thus accelerating the deterioration of materials. This issue is more relevant for more hygroscopic salt mixtures, since the deliquescence moisture of the mixture will have smaller values and the equilibrium moisture of the mirabilite-thenardite-conversion will be exceeded more often. It is to be considered, that the values of the equilibrium moisture for this transformation are not influenced by other salts. A decisive point is whether the values of the transformation falls above or below the deliquescence humidity of the mixture [Steiger.etal:2014]Title: Weathering and Deterioration
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja
 .
.
Salt mixtures where a double salt may form[edit]
Further considerations on salt mixtures can be made, especially when double salts can form that may have three of more different ions. As previously mentioned, there are both congruent and incongruent soluble double salts. A solubility diagram for the mixture Na2SO4 and MgSO4 will be considered (Fig.9), since a congruent double salt astrakanite, also referred to as blödite can form Na2Mg(SO4)2∙4H2O. The concentration of both salts are shown for a 25ºC temperature (the phases Na2SO4∙10H2O and MgSO4∙7H2O are the stable phases at this temperature). Since the double salt has a congruent solubility, it will crystallize out of the solution, having the same composition as the salt itself. From the salt formula it can be seen that it is formed by and equimolar mixture of sodium and magnesium sulfate. This is shown in the diagram by the light grey line. When reaching the saturation concentration in point A, only astrakanite will crystallize out, behaving as if it were a single salt, although it is composed of equal amounts of sodium sulfate and magnesium sulfate. The deliquescence behaviour can be similarly considered. If only astrakanite is present, it will start to absorb water vapor from the environment once it passes it staturation moisture and forming a saturated solution. If the RH continues to rise, it will result in an equimolar solution of sodium and magnesium sulfate [Steiger.etal:2014]Title: Weathering and Deterioration
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja . However if a mixture that has more magnesium sulfate (point B) in the diagram, then by evaporation of the solution the magnesium sulfate heptahydrate will crystallize out (point C), and the crystalization continues then along the C-D line. At this point D, because of the increasing content of [[sodium sulfate], astrakanite will crystallize out, ending the crystallization process.
. However if a mixture that has more magnesium sulfate (point B) in the diagram, then by evaporation of the solution the magnesium sulfate heptahydrate will crystallize out (point C), and the crystalization continues then along the C-D line. At this point D, because of the increasing content of [[sodium sulfate], astrakanite will crystallize out, ending the crystallization process.
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja
 .
.
The solubility diagram of an incongruent double salt is shown in Fig. 10. Aphthitalite (K3Na(SO4)2) is constituted by a 3:1 mixture (in terms of molality) of potassium and sodium sulfate. By evaporation of a solution with this composition at 15ºC it can be seen that potassium sulfate will crystallize as arcanite, not as aphthitalite, since from the composition of the double salt, saturation is found only with regards to arcanite. Dissolution of aphthitalite in water will not result in a saturated solution, since arcanite would crystallize out [Steiger.etal:2014]Title: Weathering and Deterioration
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja
 .
.
So far, only salt mixtures with three different ions were considered. The behaviour and the representation of mixtures with four different ions is far more complicated.
The representation can be simplified by not including water as a component. This type of representation is referred also as a Jänecke-projection [Jaenecke:1906]Title: Über eine neue Darstellungsform der wässerigen Lösungen zweier und dreier gleichioniger Salze, reziproker Salzpaare und der van't Hoffschen Untersuchungen über ozeanische Salzablagerungen.
Author: Jaenecke, E. . An example of this type of diagram is given for the mixture of Na+-K+-NO3--SO42--H2O at 25ºC (Fig. 11). The ordinate axis shows the mole fractions of the equivalent charges of the nitrate ions, the abscissa shows that corresponding to the potassium ions. All mixtures are presented by the charge equivalent mole fraction, so that the value of the ions is taken into account. In this diagram this means that various mixtures appear as partial contribution of the potassium cations or nitrate anions relative to the total amount of positive or negative charges. For example, it is clear that the amount of potassium and nitrate ions outweigh the sodium and sulfate ions at very low molar ratios. Therefore, in the four corners of the diagram are the pure four salts: at the bottom left sodium sulfate; top left sodium nitrate, top right potassium nitrate and bottom right potassium sulfate. The areas within the diagram show the stability ranges for the possible phases. They are separated by lines, representing the saturation concentration of the solutions, which correspond to the adjacent in equilibrium. This means that in any such field, only a single phase is present, in points where more lines converge there are three phases in equilibrium. At these points there are isothermic invariant phases (phase rule) [Steiger.etal:2014]Title: Weathering and Deterioration
. An example of this type of diagram is given for the mixture of Na+-K+-NO3--SO42--H2O at 25ºC (Fig. 11). The ordinate axis shows the mole fractions of the equivalent charges of the nitrate ions, the abscissa shows that corresponding to the potassium ions. All mixtures are presented by the charge equivalent mole fraction, so that the value of the ions is taken into account. In this diagram this means that various mixtures appear as partial contribution of the potassium cations or nitrate anions relative to the total amount of positive or negative charges. For example, it is clear that the amount of potassium and nitrate ions outweigh the sodium and sulfate ions at very low molar ratios. Therefore, in the four corners of the diagram are the pure four salts: at the bottom left sodium sulfate; top left sodium nitrate, top right potassium nitrate and bottom right potassium sulfate. The areas within the diagram show the stability ranges for the possible phases. They are separated by lines, representing the saturation concentration of the solutions, which correspond to the adjacent in equilibrium. This means that in any such field, only a single phase is present, in points where more lines converge there are three phases in equilibrium. At these points there are isothermic invariant phases (phase rule) [Steiger.etal:2014]Title: Weathering and Deterioration
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
As an example, a salt solution with a composition corresponding to point A falls in the stability area of glaserits (NaK3(SO4)2), so that this salt will crystallize out first upon evaporation of the solution. During crystallization and further evaporation, the composition of the solution will change following the line A-B. Once at point B, the saturation corresponds to thenardite and both salts will crystallize out. This modifies further the composition of the solution following the line B-C, reaching the area for the saturation of darapskite (Na3NO3SO4∙H2O). This is, however, and invariant point, so that only these three phases can appear together. By further evaporation of the solution, thenardite will dissolve, since its stability area does not include the C-D limit. Therefore, point D is where the final crystallization occurs [Steiger:2009a]Title: Modellierung von Phasengleichgewichten
Author: Steiger, Michael [Steiger.etal:2008c]Title: An improved model incorporating Pitzer’s equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program code
[Steiger.etal:2008c]Title: An improved model incorporating Pitzer’s equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program code
Author: Steiger, Michael; Kiekbusch, Jana; Nicolai, Andreas .
.
Author: Steiger, Michael
 , calculated according to [Steiger.etal:2008c]Title: An improved model incorporating Pitzer’s equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program code
, calculated according to [Steiger.etal:2008c]Title: An improved model incorporating Pitzer’s equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program codeAuthor: Steiger, Michael; Kiekbusch, Jana; Nicolai, Andreas
 .
.
The phase diagrams are important to show how the crystallization will proceed, as well as being practically useful because the size of the stability fields of the various phases gives an idea as to how probable it is that a particular phase will crystallize. The larger the field, the more compositions can lead to the same phase. Furthermore, it is important to know which phases can be found together: only those phases having a common limiting line or those that form at an invariant point. In the example given, it would be impossible to find mirabilite together with potassium nitrate or potassium sulfate [Steiger.etal:2014]Title: Weathering and Deterioration
Author: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
Literature[edit]
| [Arnold.etal:1991] | Arnold, Andreas; Zehnder, Konrad (1991): Monitoring Wall Paintings Affected by soluble Salts. In: Cather, Sharon (eds.): The Conservation of Wall Paintings: Proceedings of a symposium organized by the Coutrauld Institut of Art and the Getty Conservation Institute, London, July 13-16, The Getty Conservation Institute, 103-136. |  |
| [Espinosa.etal:2008] | Espinosa, R.; Franke, L.; Deckelmann, G. (2008): Model for the mechanical stress due to the salt crystallization in porous materials. In: Construction and Building Materials, 22 (7), 1350-1367, Url, 10.1016/j.conbuildmat.2007.04.013 |  |
| [Genkinger.etal:2007] | Genkinger, Selma; Putnis, Andrew (2007): Crystallisation of sodium sulfate: supersaturation and metastable phases. In: Environmental Geology, 52 (2), 329-337, 10.1007/s00254-006-0565-x |  |
| [Grossi.etal:2013] | Grossi, C.M.; Esbert, R.M.; Suarez del Rio, L.M.; Montoto, M.; Laurenzi-Tabasso, M. (2013): Acoustic emission monitoring to study sodium sulphate crystallization in monumental porous carbonate stones. In: Studies in Conservation, 42 (2), 115-125 |  |
| [Jaenecke:1906] | Jaenecke, E. (1906): Über eine neue Darstellungsform der wässerigen Lösungen zweier und dreier gleichioniger Salze, reziproker Salzpaare und der van't Hoffschen Untersuchungen über ozeanische Salzablagerungen.. In: Z. Anorg. Allg. Chem., 51 (), 132 |  |
| [Linnow.etal:2006] | Linnow, Kirsten; Zeunert, Anke; Steiger, Michael (2006): Investigation of Sodium Sulfate Phase Transitions in a Porous Material Using Humidity- and Temperature-Controlled X-ray Diffraction. In: Analytical Chemistry, 78 (13), 4683-4689, 10.1021/ac0603936 |  |
| [Price.etal:1994] | Price, Clifford A.; Brimblecomb, Peter (1994): Preventing salt damage in porous materials. In:: Preventive conservation: practice, theory and research. Preprints of the contributions to the Ottawa Congress, 12-16 September 1994, International Institute for Conservation of Historic and Artistic Works, 90-93. |  |
| [Steiger.etal:1995] | Steiger, Michael; Dannecker, Walter (1995): Hygroskopische Eigenschaften und Kristallisationsverhalten von Salzgemischen. In: Snethlage, Rolf (eds.): Jahresberichte Steinzerfall - Steinkonservierung für 1993, Verlag Ernst & Sohn, 115-128. |  |
| [Steiger.etal:1996] | Steiger, Michael; Zeunert, Anke (1996): Crystallization properties of salt mixtures: Comparison of experimental results and model calculations. In: Riederer, Josef (eds.): Proceedings of the 8th International Congress on Deterioration and Conservation of Stone, , 535-544. |  |
| [Steiger.etal:2008] | Steiger, Michael; Asmussen, Sönke (2008): Crystallization of sodium sulfate phases in porous materials: The phase diagram Na2SO4–H2O and the generation of stress. In: Geochimica et Cosmochimica Acta, 72 (17), 4291-4306, Url |  |
| [Steiger.etal:2008c] | Steiger, Michael; Kiekbusch, Jana; Nicolai, Andreas (2008): An improved model incorporating Pitzer’s equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program code. In: Construction and Building Materials, 22 (8), 1841-1850, 10.1016/j.conbuildmat.2007.04.020 |  |
| [Steiger.etal:2014] | Steiger, Michael; Charola A. Elena; Sterflinger, Katja (2014): Weathering and Deterioration. In: Siegesmund S.; Snethlage R. (eds.): Stone in Architecture, Springer Verlag Berlin Heidelberg, 223-316, 10.1007/978-3-642-45155-3_4. |  |
| [Steiger:2009a] | Steiger, Michael (2009): Modellierung von Phasengleichgewichten. In: Schwarz, Hans-Jürgen; Steiger, Michael (eds.): Salzschäden an Kulturgütern: Stand des Wissens und Forschungsdefizite, Ergebnisse des DBU Workshops im Februar 2008 in Osnabrück, Deutsche Bundesstiftung Umwelt, Eigenverlag, 80-99. |   |
| [Xu.etal:1999] | Xu B., Schweiger G. (1999): In-situ Raman observations of phase transformation of Na2SO4 during the hydration/dehydration cycles on single levitated microparticle.. In: J. Aerosol. Sci., (), 379-380 |  |